题目内容
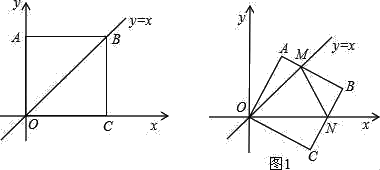
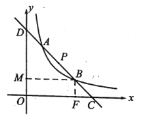
【题目】已知直线l过点P(2, 2),且与函数y=![]() (x>0)的图象相交于A, B两点,与x轴、y轴分别交于点C, D,如图所示,四边形OFBM为矩形,面积为3.
(x>0)的图象相交于A, B两点,与x轴、y轴分别交于点C, D,如图所示,四边形OFBM为矩形,面积为3.
(1)求k的值;
(2)当点B的横坐标为3时,求直线l的解析式及线段BC的长.
【答案】(1)k=3;(2)直线l解析:y=-x+4,BC=![]() ;
;
【解析】
(1)利用待定系数法即可解决问题;
(2)求出B、C两点坐标,求出直线BC的解析式即可解决问题.
解:(1)设点B的坐标为(x,y),由题意得:BF=y,BM=x,
∵矩形OMBF的面积为3,
∴xy=3,
∵B在双曲线y=![]() 上,
上,
∴k=3;
(2)∵点B的横坐标为3,点B在双曲线上,
∴点B的坐标为(3,1),
设直线l的解析式为y=ax+b,
∵直线l过点P(2,2),B(3,1),
∴![]() 解得
解得![]() ,
,
∴直线l的解析式为y=-x+4,
∵直线l与x轴交于点C(4,0),
∴BC=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E |
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |
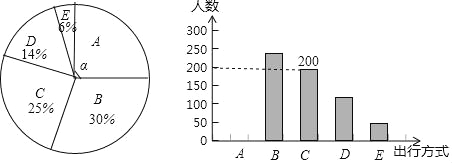
根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有 人,其中选择B类的人数有 人;
(2)在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.