题目内容
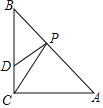
【题目】如图,在正方形ABCD中,E、F分别是BC、CD边上的点,∠EAF=45°.
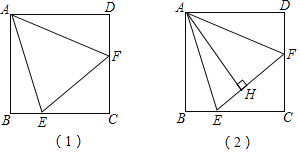
(1)如图(1),试判断EF,BE,DF间的数量关系,并说明理由;
(2)如图(2),若AH⊥EF于点H,试判断线段AH与AB的数量关系,并说明理由.
【答案】(1)BE+DF=EF理由见解析;(2)AH=AB,理由见解析
【解析】
(1)延长FD到G,使DG=BE,连接AG,证△GDA≌△EBA,△GAF≌△EAF,根据全等三角形的性质得出GD+DF=BE+DF=EF进而求出即可;
(2)把△ADF绕点A顺时针旋转90°得到△ABQ,如图,根据旋转的性质得AQ=AF,∠FAQ=90°,∠ABQ=∠D=90°,则可判断点Q在CB的延长线上,由∠EAF=45°得到∠QAE=90°﹣∠EAF=45°,然后根据“SAS”判断△AEQ≌△AEF,得到EQ=FE,再根据全等三角形对应边上的高相等得到结论.
解:(1)BE+DF=EF;
理由如下:
如图1,延长FD到G,使DG=BE,连接AG,

∵在△GDA和△EBA中,
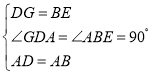 ,
,
∴△GDA≌△EBA(SAS),
∴AG=AE,∠GAD=∠EAB,
故∠GAF=45°,
在△GAF和△EAF中,
∵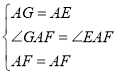 ,
,
∴△GAF≌△EAF(SAS),
∴GF=EF,
即GD+DF=BE+DF=EF;
(2)AH=AB,
理由如下:
∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∴把△ADF绕点A顺时针旋转90°得到△ABQ,如图2,

∴AQ=AF,∠FAQ=90°,∠ABQ=∠D=90°,
而∠ABC=90°,
∴点Q在CB的延长线上,
∵∠EAF=45°,
∴∠QAE=90°﹣∠EAF=45°,
∴∠EAF=∠QAE,
在△AEQ和△AEF中,
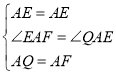 ,
,
∴△AEQ≌△AEF(SAS),
∴EQ=EF,
∵AB⊥EQ,AH⊥FE,
∴AB=AH.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案