Question

【题目】如图，点E是菱形ABCD对角线CA的延长线上任意一点，以线段AE为边作一个菱形AEFG，且菱形AEFG∽菱形ABCD，连接EB，GD．

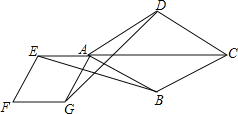
（1）求证：EB＝GD；

（2）若∠DAB＝60°，AB＝2，AG＝，求GD的长．

Answer 1

【答案】（1）见解析；（2）GD＝．

【解析】

（1）用SAS证明△AEB≌△AGD即可得到EB＝GD；

（2）连接BD.由（1）可知，求出EB即可得到GD的长.依次求出BP、AP、EP的长即可解决问题.

（1）证明：∵菱形AEFG∽菱形ABCD，

∴∠EAG＝∠BAD，

∴∠EAG+∠GAB＝∠BAD+∠GAB，

∴∠EAB＝∠GAD，

∵AEFG是菱形，ABCD是菱形，

∴AE＝AG，AB＝AD，

∴△AEB≌△AGD，

∴EB＝GD；

（2）解：连接BD交AC于点P，则BP⊥AC，

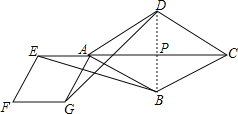
∵∠DAB＝60°，

∴∠PAB＝30°，

∴BP＝AB＝1，

AP＝＝，AE＝AG＝，

∴EP＝2，

∴EB＝＝＝，

∴GD＝．