题目内容
【题目】如图,已知在矩形ABCD中,M是AD边的中点,BM与AC垂直,交直线AC于点N,连接DN,则下列四个结论中:①CN=2AN;②DN=DC;③tan∠CAD=![]() ;④△AMN∽△CAB.正确的有( )
;④△AMN∽△CAB.正确的有( )
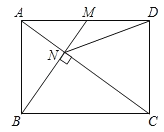
A.①②③④B.①②③C.①②④D.②③④
【答案】C
【解析】
通过证明△AMN∽△CBN,可得![]() ,可证CN=2AN;过D作DH∥BM交AC于G,可证四边形BMDH是平行四边形,可得BH=MD=
,可证CN=2AN;过D作DH∥BM交AC于G,可证四边形BMDH是平行四边形,可得BH=MD=![]() BC,由直角三角形的性质和等腰三角形的性质可得DN=DC;通过证明△ABM∽△BCA,可得
BC,由直角三角形的性质和等腰三角形的性质可得DN=DC;通过证明△ABM∽△BCA,可得![]() ,可求AB=
,可求AB=![]() BC,即可得tan∠DAC=
BC,即可得tan∠DAC=![]() ;由平行线性质可得∠DAC=∠ACB,∠ABC=∠ANM=90°,可证△AMN∽△CAB,则可求解.
;由平行线性质可得∠DAC=∠ACB,∠ABC=∠ANM=90°,可证△AMN∽△CAB,则可求解.
∵AD//BC,
∴△AMN∽△CBN,
∴![]() ,
,
∵M是AD边的中点,
∴AM=MD=![]() AD=
AD=![]() BC,
BC,
∴![]() ,
,
∴CN=2AN,故①正确;
如图,过D作DH//BM交AC于G,
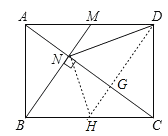
∵DH//BM,BM⊥AC,
∴DH⊥AC,
∵DH//BM,AD//BC,
∴四边形BMDH是平行四边形,
∴BH=MD=![]() AD=
AD=![]() BC,
BC,
∴BH=CH,
∵∠BNC=90°,
∴NH=HC,
∵DH⊥AC,
∴DH是NC的垂直平分线,
∴DN=CD,故②正确;
∵AD//BC,
∴∠DAC=∠BCA,
∵∠BAC+∠ACB=90°,∠DAC+∠AMB=90°,
∴∠BAC=∠AMB,
∵∠BAM=∠ABC,
∴△ABM∽△BCA,
∴![]() ,
,
∴AB2=![]() BC2,
BC2,
∴AB=![]() BC,
BC,
∵tan∠DAC=tan∠ACB=![]() ,
,
∴tan∠DAC=![]() ,故③错误,
,故③错误,
∵四边形ABCD是矩形,
∴AD//BC,∠ABC=90°,AD=BC,
∴∠DAC=∠ACB,
∵∠ABC=∠ANM=90°,
∴△AMN∽△CAB,故④正确;
故选:C.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目