题目内容
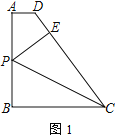
【题目】如图,O为Rt△ABC的直角边AC上一点,以OC为半径的圆与斜边AB相切于点D,P是弧CD上任意一点,过点P作⊙O的切线,交BC于点M,交AB于点N,已知AB=5,AC=4.
(1)△BMN的周长等于多少;
(2)⊙O的半径.

【答案】(1)△BMN的周长为6,(2)⊙O的半径为1.5.
【解析】
(1)由勾股定理可求得是BC,再证得BC为圆的切线,则可求得BC和BD的长,由切线长定理可求得PM=CM、PN=ND,则可求得答案;
(2)连接OD,设半径为r,则AO=4-r,AD=2,在Rt△AOD中,由勾股定理可列方程,可求得r.
(1)在Rt△ABC中,AB=5,AC=4,
∴BC=3,
∵AC⊥BC,
∴BC为⊙O的切线,
∵AB为⊙O的切线,
∴BD=BC=3,
∵MN为⊙O的切线,
∴PM=CM,PN=DN,
∴BM+BN+MN=BM+PM+BN+PN=BM+MC+BN+ND=BC+BD=3+3=6,
即△BMN的周长为6,
故答案为:6;
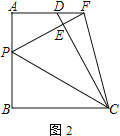
(2)如图,连接OD,
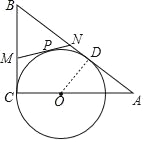
∵AB为⊙O的切线,
∴OD⊥AB,
设半径为r,则AO=AC﹣r=4﹣r,AD=AB﹣BD=5﹣3=2,
在Rt△AOD中,由勾股定理可得r2+22=(4﹣r)2,解得r=1.5,
∴⊙O的半径为1.5.

【题目】已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.
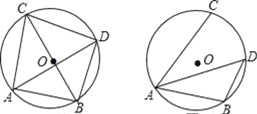
(Ⅰ)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(Ⅱ)如图②,若∠CAB=60°,求BD的长.
【题目】某青年旅社有60间客房供游客居住,在旅游旺季,当客房的定价为每天200元时,所有客房都可以住满.客房定价每提高10元,就会有1个客房空闲,对有游客入住的客房,旅社还需要对每个房间支出20元/每天的维护费用,设每间客房的定价提高了x元.
(1)填表(不需化简)
入住的房间数量 | 房间价格 | 总维护费用 | |
提价前 | 60 | 200 | 60×20 |
提价后 |
|
|
|
(2)若该青年旅社希望每天纯收入为14000元且能吸引更多的游客,则每间客房的定价应为多少元?(纯收入=总收入﹣维护费用)