题目内容
【题目】如图1,数轴上的点A,B.C依次表示数-2,x,4.某同学将刻度尺如图2放置,使刻度尺上的数字0对齐数轴上的点B,发现点A对齐刻度1.8cm,点C对齐刻度5.4cm.
(1)AC= 个单位长度;由图可知数轴上的一个单位长度对应刻度尺上的 cm;数轴上的点B表示数 ;

(2)已知T是数轴上一点(不与点A、点B、点C重合),点P表示的数是t,点P是线段BT的三等分点,且TP=2BP.
①如图3,当-2<t<4时,试试猜想线段CT与AP的数量关系,并说明理由;
②若|2BT-3AP|=1,请直接写出所有满足条件的t的值.

【答案】(1)6,0.6,-5;(2)猜想:AP=![]() CT,证明见解析;(3)t=-15或t=-13或t=-
CT,证明见解析;(3)t=-15或t=-13或t=-![]() 或t=-
或t=-![]() .
.
【解析】
(1)根据两点间的距离解答即可;
(2)①先根据P是线段BT的三等分点得:BP=![]() BT=
BT=![]() (t+5),再根据两点间的距离分别表示CT和AP的长解答即可;
(t+5),再根据两点间的距离分别表示CT和AP的长解答即可;
②分四种情况进行讨论,根据|2BT-3AP|=1列方程解答即可.
(1)AC=4-(-2)=6(个单位长度),
AC=5.4-1.8=3.6cm,
![]() ,
,
即数轴上的一个单位长度对应刻度尺上的0.6cm,
∴1.8=0.6(-2-x),
x=-5,
即数轴上的点B表示-5,
故答案为:6;0.6;-5;
(2)①如图3,猜想:![]() ,
,
理由是:∵TP=2BP,
∴![]() ,
,
∵AB=-2-(-5)=3,
∴![]() ,
,
∴CT=4-t,
∴![]() ;
;
②分四种情况:
i)如图4,当t>4,则点P在A的右边,

∴BT=t+5,![]() ,
,
∵|2BT-3AP|=1,
∴2BT-3AP=1或2BT-3AP=-1,
![]() 或
或![]() ,
,
解得:t=-13(不符合题意),t=-15(不符合题意),
ii)如图3,当-2<t<4时,
∵|2BT-3AP|=1,
∴2BT-3AP=1或2BT-3AP=-1,
由①得:![]() ,
,
解得:![]() ,
,
或![]() ,
,
解得:![]() (不符合题意),
(不符合题意),
iii)如图5,当-5<t<-2时,

∴BT=t+5,![]() ,
,
∵|2BT-3AP|=1,
∴2BT-3AP=1或2BT-3AP=-1,
由①得:![]() ,
,
解得:![]() (不符合题意),
(不符合题意),
或![]() ,
,
解得:![]() ,
,
iiii)如图6,当t<-5时,

∴BT=-5-t,![]() ,
,
∵|2BT-3AP|=1,
∴2BT-3AP=1或2BT-3AP=-1,
![]() ,
,
解得:t=-15,
或![]() ,
,
解得:t=-13,
综上,t=-15或t=-13或![]() 或
或![]() .
.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案【题目】在硬地上抛掷一枚图钉,通常会出现两种情况:

下面是小明和同学做“抛掷图钉实验”获得的数据:
抛掷次数n | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 |
针尖不着地的频数m | 63 | 120 | 186 | 252 | 310 | 360 | 434 | 488 | 549 | 610 |
针尖不着地的频率 | 0.63 | 0.60 | 0.63 | 0.60 | 0.62 | 0.61 |
(1)填写表中的空格;
(2)画出该实验中,抛掷图钉钉尖不着地频率的折线统计图;

(3)根据“抛掷图钉实验”的结果,估计“钉尖着地”的概率为 .
【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表: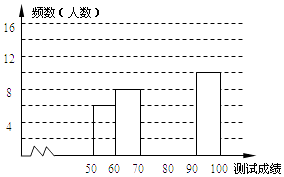
请结合图表完成下列各题:
(1)①表中a的值为 , 中位数在第组;
②频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
(3)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
组别 | 成绩x分 | 频数(人数) |
第1组 | 50≤x<60 | 6 |
第2组 | 60≤x<70 | 8 |
第3组 | 70≤x<80 | 14 |
第4组 | 80≤x<90 | a |
第5组 | 90≤x<100 | 10 |