题目内容
【题目】某校初三年级有四个班,每班挑选乒乓球男女队员各一人,组成年级混合双打代表队,那么四对混合双打中,没有一队选手是同班同学的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
首先根据乘法公式,求得4男4女组成四队混合双打的情况共有24种,然后设一、二、三、四班的男、女选手分别为A1、B1、A2、B2、A3、B3、A4、B4,则可列出四队混合双打中,没有一对选手是同班同学的情况,再根据概率公式,即可求得答案.
解:∵先把四个女运动员任意排列,设为A B C D,
和A配合的男运动员有4个选择;
和B配合的男运动员剩下3种选择;
和C配合的男运动员剩下2种选择;
最后一个和D配合.
所以总共有24种.
∴4男4女组成四队混合双打的情况共有:4×3×2=24种,
设一、二、三、四班的男、女选手分别为A1、B1、A2、B2、A3、B3、A4、B4,则四队混合双打中,没有一对选手是同班同学的情景如下:
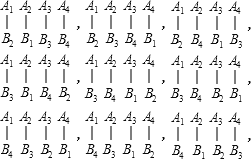
由上得共有9种情形.
故四对混合双打中,没有一对选手是同班同学的概率是:![]() .
.
故选C.

练习册系列答案
相关题目