题目内容
【题目】某中学计划购买A型和B型课桌凳共200套.经招标,购买一套A型课桌凳比购买一套B型课桌凳少用40元,且购买4套A型和5套B型课桌凳共需1820元.
(1)求购买一套A型课桌凳和一套B型课桌凳各需多少元?
(2)学校根据实际情况,要求购买这两种课桌凳总费用不能超过40880元,并且购买A型课桌凳的数量不能超过B型课桌凳数量的![]() ,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
【答案】(1) 购买一套A型课桌凳和一套B型课桌凳各需180元和220元.
(2) 共有3种方案,总费用最低方案是购买A型80套,购买B型120套
【解析】试题分析: (1)根据购买一套A型课桌凳比购买一套B型课桌凳少用40元,以及购买4套A型和5套B型课桌凳共需1820元,得出等式方程求出即可;
(2)利用要求购买这两种课桌凳总费用不能超过40880元,并且购买A型课桌凳的数量不能超过B型课桌凳数量的![]() ,得出不等式组,求出a的值即可,再利用一次函数的增减性得出答案即可.
,得出不等式组,求出a的值即可,再利用一次函数的增减性得出答案即可.
试题解析:
(1)设A型每套![]() 元,B型每套(
元,B型每套(![]() )元
)元
∴![]()
∴![]()
即购买一套A型课桌凳和一套B型课桌凳各需180元和220元。
(2)设A型课桌凳![]() 套,则购买B型课桌凳(
套,则购买B型课桌凳(![]() )套
)套
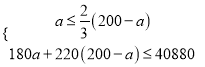
解得![]()
∵![]() 为整数,所以
为整数,所以![]() =78,79,80
=78,79,80
所以共有3种方案。
当a=78时,180a+220(200—a )= 40880
当a=79时,180a+220(200—a )= 40840
当a=80时,180a+220(200—a )= 40800总费用最低,此时200- ![]() =120
=120
即总费用最低方案是购买A型80套,购买B型120套。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目