题目内容
【题目】如图,已知M是△ABC的边AB的中点,D是MC的延长线上一点,满足∠ACM=∠BDM.
(1)求证:AC=BD;
(2)若∠BMC=60°,求![]() 的值.
的值.

【答案】(1)证明见解析(2)2
【解析】
(1)证明:延长CM至F,使MF=CM,连接AF、BF,根据对角线互相平分的四边形是平行四边形得到四边形AFBC是平行四边形,根据平行四边形的性质得到∠BFM=∠ACM,等量代换得到∠BFM=∠BDM,即可证明BD=BF=AC;
(2) 延长CM至点E,使EM=CD,连结AE,证明△ACE≌△BDM,根据全等三角形的性质得到AE=BM=AM,又∠BMC=60° ,证明△AEM是等边三角形,得到AB=2AM=2ME=2CD,即可求解.
(1)证明:延长CM至F,使MF=CM,连接AF、BF
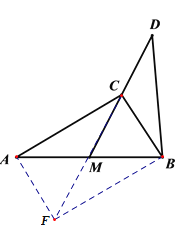
∵四边形AFBC中对角线CF、AB互相平分
∴四边形AFBC是平行四边形
∴∠BFM=∠ACM,
∵∠ACM=∠BDM.
∴∠BFM=∠BDM,
∴BD=BF=AC
(2)解:延长CM至点E,使EM=CD,连结AE
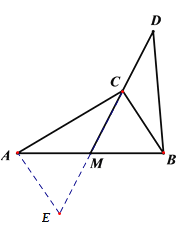
∴在△ACE和△BDM中
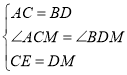
∴△ACE≌△BDM
∴AE=BM=AM
又∠BMC=60°
∴∠AME=60°
∴△AEM是等边三角形
∴AB=2AM=2ME=2CD
∴![]() .
.

练习册系列答案
相关题目