题目内容
【题目】阅读材料：各类方程的解法
求解一元一次方程，根据等式的基本性质，把方程转化为x=a的形式。求解二元一次方程组，把它转化为一元一次方程来解：求解一元二次方程，把它转化为两个一元一次方程来解。求解分式方程，把它转化为整式方程来解。各类方程的解法不尽相同，但是它们有一个共同的基本数学思想--转化，把未知转化为已知。
用“转化”的数学思想，我们还可以解一些新的方程。例如，一元三次方程
，可以通过因式分解把它转化为
，解方程
和
，可得方程的解。
（1）问题：方程的解是
，
_____，
_____。
（2）拓展：用“转化”思想求方程
的解。
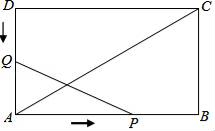
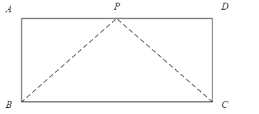
（3）应用：如图，已知矩形草坪ABCD的长
，宽
，小华把一根长为10m的绳子的一端固定在点B，沿草坪边沿BA，AD走到点P处，把长绳PB段拉直并固定在点P，然后沿草坪边沿PD、DC走到点C处，把长绳剩下的一段拉直，长绳的另一端恰好落在点C。求AP的长。
【答案】（1）2，-1; （2）1，3 ; （3）3m.
【解析】
（1）因式分解多项式，然后得结论；
（2）两边平方，把无理方程转化为整式方程，求解，验根即可；
（3）设AP的长为xm，根据勾股定理和BP+CP=10，可列出方程，由于方程含有根号，两边平方，把无理方程转化为整式方程，求解即可.
（1）x3-x2-2x=0，
x（x2-x-2）=0，
x（x-2）（x+1）=0
所以x=0或x-2=0或x+1=0
∴x1=0，x2=2，x3=-1；
故答案为： 2，-1；
（2）
方程的两边平方，得4x-3=x2
即x2-4x+3=0
（x-3）（x-1）=0
∴x-3=0或x-1=0
∴x1=3，x2=1，
当x=3或1时,
有意义，故是方程的解.
（3）因为四边形ABCD是矩形，
所以∠A=∠D=90°，AB=CD=4m,
设AP=xm，则PD=（6-x）m
因为BP+CP=10，BP=
,CP=
,
所以
=10-
两边平方，得16+(6-x)2=100-20+x2+16
整理，得3x+16=5,
两边平方并整理，得x2-6x+9=0
即（x-3）2=0
所以x=3．
经检验，x=3是方程的解．
答：AP的长为3m．
