题目内容
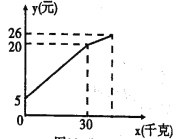
【题目】如图，在平面直角坐标系中，△ABC的边BC在x轴上，顶点A在y轴的正半轴上，OA=2，OB=1，OC=4．
（1）求过A、B、C三点的抛物线的解析式；
（2）设点M是x轴上的动点，试问：在平面直角坐标系中，是否存在点N，使得以点A，B，M，N为顶点的四边形是菱形？若存在，直接写出点N的坐标；若不存在，说明理由；
（3）若抛物线对称轴交x轴于点P，在平面直角坐标系中，是否存在点Q，使△PAQ是以PA为腰的等腰直角三角形？若存在，写出所有符合条件的点Q的坐标，选择一种情况加以说明；若不存在，说明理由．
【答案】（1）y=﹣
x2+
x+2（2）（0，﹣2），（
，2），（﹣
，2），（﹣2.5，2）（3）（
， 
）
【解析】试题分析：（1）设抛物线的解析式为y=ax2+bx+c．将点A、B、C的坐标代入得到关于a、b、c的方程，从而可求得a、b、c的值；
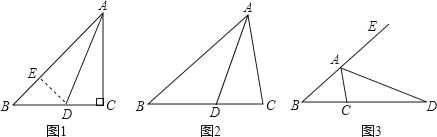
（2）分为AB为菱形的边和AB为菱形的对角共可画出4种不同的图形，然后依据菱形对边平行，对角线互相平分的性质确定出点N的坐标即可；
（3）如图5所示：分别以点A和点P为直角的顶点作出等腰直角△APQ，然后由抛物线的对称轴方程求得点P的坐标，过点Q1作Q1M⊥x轴，垂足为M．
然后证明△AOP≌△PMQ1，由全等三角形的性质可求得Q1M=OP=
，PM=OA=2，于是可求得点Q1的坐标．
试题解析：（1）由题意可知；A（0，2）、B（﹣1，0）、C（4，0）．
设过A、B、C三点的抛物线的解析式为y=ax2+bx+c．则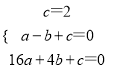
，解得：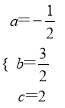 
所以抛物线的解析式为y=﹣
x2+
x+2．
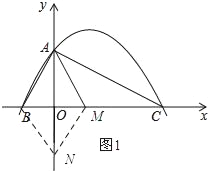
（2）如图1所示：
∵四边形ABNM为菱形，
∴OA=ON．
∴点N的坐标为（0，﹣2）．
如图2所示：
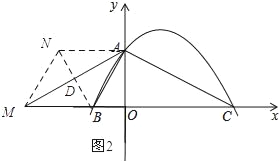
由勾股定理可知：AB=
．
∵四边形ABMN为菱形，
∴NA∥BM，AN=AB，
∴点N的坐标为（﹣
，2）．
如图3所示；
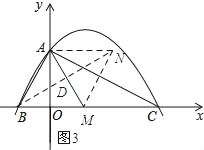
∵四边形ABMN为菱形，
∴NA∥BM，AN=AB．
∴点N的坐标为（
，2）．
如图4所示：
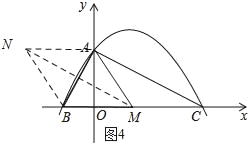
∵四边形ABMN为菱形，
∴NA∥BM，AN=NB．
设点N的坐标为（x，2）．由两点间的距离公式可知：（x+1）2+22=x2．
解得：x=﹣2.5．
∴点N的坐标为（﹣2.5，2）．
∴点N的坐标为（0，﹣2），（
，2），（﹣
，2），（﹣2.5，2）．
（3）如图5所示：
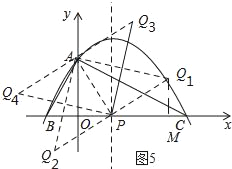
使△PAQ是以PA为腰的等腰直角三角形的所有符合条件的点Q的坐标为Q1（
， 
），Q2（﹣
，﹣
），Q3（2， 
），Q4（﹣2， 
）．
说明Q1：过点Q1作Q1M⊥x轴，垂足为M．
∵x=﹣
，
∴P（
，0）．
∴OP=
．
由题意得；∠APQ1=90°，PA=PQ1．
∴∠OPA+∠CPQ1=90°．
∵∠APO+∠OAP=90°，
∴∠OAP=∠MPQ1．
在△AOP和△PMQ1中，
，
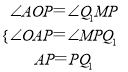∴△AOP≌△PMQ1．
∴Q1M=0P=
，PM=OA=2
∴OM=OP+PM=
+2=
．
∴点Q1的坐标为（
， 
）．
