题目内容
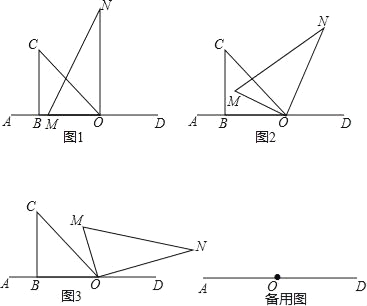
【题目】如图1,已知直线PQ∥MN,点A、B分别在直线MN、PQ上,射线AM绕点A以5°/秒的速度按顺时针开始旋转,旋转至与AN(或AM)重合后便立即回转,射线BQ绕点B以2°/秒的速度按顺时针开始旋转,旋转至与BP重合后便停止转动,旋转后的射线分别记为AM'和BQ'.
(1)若射线BQ先转动30秒,射线AM才开始转动,在射线AM第一次到达AN之前,射线AM转动几秒后AM'∥BQ';
(2)若射线AM,BQ同时转动t秒,在射线BQ停止转动之前,记射线AM'与BQ'交于点H,若∠AHB=90°,求t的值;
(3)射线AM,BQ同时转动,在射线AM第一次到达AN之前,记射线AM'与BQ'交于点K,过K作KC⊥AK交PQ于点C,如图2,若∠BAN=30°,则在旋转过程中,∠BAK与∠BKC有何数量关系?并说明理由.

【答案】(1)t=10s时,BQ′∥AM′;(2)满足条件的t的值为30秒或90秒.(3)![]()
【解析】
(1)当∠MAM′=∠QBQ′时,BQ′∥AM′,延长构建方程即可解决问题;
(2)根据点Q的运动时间t=90秒,分三种情形分别构建方程求解即可;
(3)如图3中,设∠KAB=x,∠BKC=y.设直线CK交MN于G.利用平行线的性质,构建方程组确定x与y之间的关系即可.
(1)由题意当5t=30+2t时,BQ′∥AM′,
∴t=10s时,BQ′∥AM′.
(2)∵点Q的运动时间t=![]() =90(秒),
=90(秒),
分三种情形:①射线AM第一次到达AN之前:如图1中,

当∠NAM′+∠QBQ′=90°时,∠AHB=90°,
则有2t+180°﹣5t=90°,
解得t=30(秒),
②射线AM返回途中:如图2中,

当∠MAM′+∠PBQ′=90°时,∠AHB=90°,
则有180°﹣2t+180°﹣(5t﹣180°)=90°,
解得t=![]() (秒)(不合题意舍弃),
(秒)(不合题意舍弃),
③射线AM第二次到达AN之前,如图2中,
当∠MAM′+∠PBQ′=90°时,∠AHB=90°,
则有180°﹣2t+(5t﹣360°)=90°,
解得t=90(秒),
综上所述,满足条件的t的值为30秒或90秒.
(3)如图3中,设∠KAB=x,∠BKC=y.设直线CK交MN于G.

∵AK⊥KC,
∴∠AKG=90°,
∴∠KAG+∠AGK=90°,
∵PQ∥MN,
∴∠AGK=∠QCK,
∴180°﹣5t+2t+y=90°,
∴t=30°﹣![]() y,
y,
∵x=30°﹣(180°﹣5t),
∴x=5t﹣150°,
∴x=5(30°﹣![]() y)﹣150°,
y)﹣150°,
∴x=![]() y,
y,
∴∠KAB=![]() ∠BKC.
∠BKC.

 53随堂测系列答案
53随堂测系列答案