题目内容
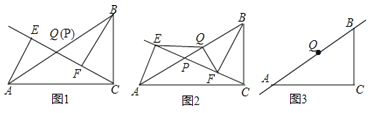
【题目】如图,矩形![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() 轴、
轴、![]() 轴上, 点
轴上, 点![]() 坐标为
坐标为![]() , 连接
, 连接![]() ,将矩形
,将矩形![]() 沿
沿![]() 折叠,点
折叠,点![]() 的对应点为点
的对应点为点![]() ,则点
,则点![]() 的坐标为_____(用含
的坐标为_____(用含![]() 的式子表示).
的式子表示).
【答案】![]()
【解析】
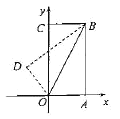
过点D做DE⊥x轴,垂足为E,交BC延长线于点F.证明△OED∽△DFB,相似比为1:2,设DE=m,表示各线段关系,求出m,进而求出点![]() 的坐标.
的坐标.
解:如图,过点D做DE⊥x轴,垂足为E,交BC延长线于点F.
∵矩形![]() 中,点
中,点![]() 坐标为
坐标为![]() ,
,
∴OA=k,AB=2k.
∵矩形![]() 沿
沿![]() 折叠,
折叠,
∴△OBD≌△OBA,
∴OD= OA=k,BD=BA=2k,∠ODB=∠OAB=90°,
∴∠FDB+∠EDO=90°.
∵∠EOD+∠EDO=90°,
∴∠EOD=∠FDB.
∵∠F=∠DEO=90°,
∴△OED∽△DFB,
∴![]() .
.
设DE=m,则BF=2m,OE=2m-k,
∴2k-m=2(2m-k)
∴![]() ,
,
∴![]()
∴点D坐标为:![]() .
.
故答案为:![]() .
.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
【题目】学校开展的“书香校园”活动受到同学们的广泛关注,为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如图不完整的统计图表.
学生借阅图书的次数统计表:
借阅图书的次数 |
|
|
|
|
|
人数 |
|
|
|
|
|

请你根据统计图表中的信息,解答下列问题:
(1)![]() ,
,![]() ;
;
(2)该调查统计数据的中位数是 ,众数是 ;
(3)若该校共有![]() 名学生,根据调查结果,估计该校学生在一周内借阅图书
名学生,根据调查结果,估计该校学生在一周内借阅图书![]() 次及以上的人数.
次及以上的人数.