题目内容
【题目】将平行四边形纸片![]() 按如图方式折叠,使点
按如图方式折叠,使点![]() 与
与![]() 重合,点
重合,点![]() 落到
落到![]() 处,折痕为
处,折痕为![]() .
.

(1)求证:![]() ;
;
(2)连结![]() ,判断四边形
,判断四边形![]() 是什么特殊四边形?证明你的结论.
是什么特殊四边形?证明你的结论.
【答案】(1)证明见解析;(2)四边形AECF是菱形.证明见解析.
【解析】
试题分析:(1)根据平行四边形的性质及折叠的性质我们可以得到∠B=∠D′,AB=AD′,∠1=∠3,从而利用ASA判定△ABE≌△AD′F;
(2)四边形AECF是菱形,我们可以运用菱形的判定,有一组邻边相等的平行四边形是菱形来进行验证.
试题解析:(1)由折叠可知:∠D=∠D′,CD=AD′,
∠C=∠D′AE.
∵四边形ABCD是平行四边形,
∴∠B=∠D,AB=CD,∠C=∠BAD.
∴∠B=∠D′,AB=AD′,∠D′AE=∠BAD,
即∠1+∠2=∠2+∠3.
∴∠1=∠3.
在△ABE和△AD′F中
∵
∴△ABE≌△AD′F(ASA).
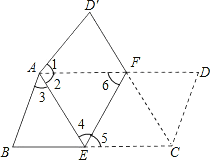
(2)四边形AECF是菱形.
证明:由折叠可知:AE=EC,∠4=∠5.
∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠5=∠6.
∴∠4=∠6.
∴AF=AE.
∵AE=EC,
∴AF=EC.
又∵AF∥EC,
∴四边形AECF是平行四边形.
又∵AF=AE,
∴平行四边形AECF是菱形.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
【题目】近年来,我国持续大面积的雾霾天气让环保和健康问题成为焦点,为进一步普及环保和健康知识,我市某校举行了“建设宜居成都,关注环境保护”的知识竞赛,某班学生的成绩统计如下:
成绩(分) | 60 | 70 | 80 | 90 | 100 |
人数 | 4 | 8 | 12 | 11 | 5 |
则该班学生成绩的众数和中位数分别是( )
A. 70分,80分 B. 80分,80分 C. 90分,80分 D. 80分,90分