Question

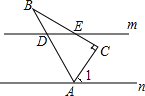
【题目】如图，BE，CE平分△ABC的两个外角，且交于点E，∠A＝80°.

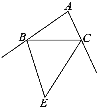
(1)∠E的度数是多少？

(2)若∠ABC＝35°，写出四边形ABEC各内角的度数．

Answer 1

【答案】（1）∠E＝50°；（2）四边形ABEC各内角的度数为∠A＝80°，∠ABE＝107.5°，∠E＝50°，∠ACE＝122.5°.

【解析】

（1）由BE、CE是两外角的平分线，得到根据三角形的外角的性质和三角形的内角和得到+∠ABC）=180°，于是得到即可得到结论；

（2）由∠ABC=35°，根据邻补角的定义得到∠DBC=180°-∠ABC=145°，由BE平分∠DBC，得到,于是得到,于是得到,然后根据四边形的内角和得到结果．

解：(1)如图．∵BE，CE平分△ABC的两个外角，

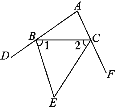
∴∠1＝∠CBD，∠2＝∠BCF.

∵∠CBD＝∠A＋∠ACB，∠BCF＝∠A＋∠ABC，

∴∠1＝ (∠A＋∠ACB)，∠2＝ (∠A＋∠ABC)．

∵∠E＋∠1＋∠2＝180°，

∴∠E＋ (∠A＋∠ACB)＋ (∠A＋∠ABC)＝180°，

即∠E＋∠A＋ (∠A＋∠ACB＋∠ABC)＝180°.

∵∠A＋∠ACB＋∠ABC＝180°，∴∠E＋∠A＝90°，

∴∠E＝90°－∠A＝50°.

(2)∵∠ABC＝35°，∴∠CBD＝180°－∠ABC＝145°.

∵BE平分∠CBD，∴∠1＝72.5°，

∴∠ABE＝35°＋72.5°＝107.5°，

∴∠ACE＝360°－∠A－∠E－∠ABE＝122.5°，

∴四边形ABEC各内角的度数为：∠A＝80°，

∠ABE＝107.5°，∠E＝50°，∠ACE＝122.5°.