题目内容
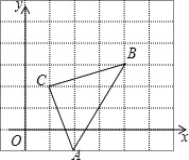
【题目】如图,在△ABC中,点E是边AC上一点,线段BE垂直于∠BAC的平分线于点D,点M为边BC的中点,连接DM.
(1)求证: DM=![]() CE;
CE;
(2)若AD=6,BD=8,DM=2,求AC的长.

【答案】(1)见解析 (2)AC=14
【解析】
(1)证△BAD≌△EAD,推出AB=AE,BD=DE,根据三角形的中位线性质得出DM=![]() CE即可;
CE即可;
(2)根据勾股定理求出AB,求出AE,根据三角形的中位线求出CE,即可得出答案.
∵AD⊥BE,
∴∠ADB=∠ADE=90°,
∵AD为∠BAC的平分线,
∴∠BAD=∠EAD,
在△BAD和△EAD中,
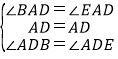 ,
,
∴△BAD≌△EAD(SAS),
∴AB=AE,BD=DE,
∵M为BC的中点,
∴DM=![]() CE
CE
(2)∵在Rt△ADB中,∠ADB=90°,AD=6,BD=8,
∴由勾股定理得:AE=AB=![]() ,
,
∵DM=2,DM=![]() CE,
CE,
∴CE=4,
∴AC=10+4=14.

练习册系列答案
相关题目
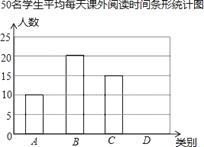
【题目】某校七年级举行“数学计算能力”比赛,比赛结束后,随机抽查部分学生的成绩,根据抽查结果绘制成如下的统计图表
组别 | 分数x | 频数 |
A | 40≤x<50 | 20 |
B | 50≤x<60 | 30 |
C | 60≤x<70 | 50 |
D | 70≤x<80 | m |
E | 80≤x<90 | 40 |
根据以上信息解答下列问题:
(1)共抽查了 名学生,统计图表中,m= ,请补全直方图;
(2)求扇形统计图中“B组”所对应的圆心角的度数;
(3)若七年级共有800名学生,分数不低于60分为合格,请你估算本次比赛全年级合
格学生的人数