题目内容
如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD = 2,将腰CD以D为中心逆时针旋转90°至DE,连接AE、CE,△ADE的面积为3,则BC的长为 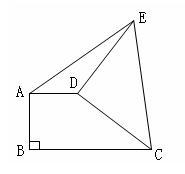

5
过D、E分别作DN⊥AD、EM⊥AD,交AD的延长线与M,交BC与N。
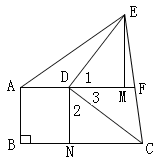
∵AD∥BC ,AB⊥BC,∴四边形ABND是矩形,∴AD=BN=2 ∵将腰CD以D为中心逆时针旋转90°∴∠1+∠3=90°∵DN⊥AD ∴∠2+∠3=90°∴∠1=∠2,∵DN⊥AD,AD∥BC ∴DN⊥BC ,又∵EM⊥AD ∴∠EMD=∠CND=90°又∵DC=DE ∴△DCN≌△DEM(AAS)∴ME=CN S△ADE= 即3=
即3=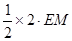 ,∴EM=CN=3 ∴BC=BN+CN=2+3=5
,∴EM=CN=3 ∴BC=BN+CN=2+3=5

∵AD∥BC ,AB⊥BC,∴四边形ABND是矩形,∴AD=BN=2 ∵将腰CD以D为中心逆时针旋转90°∴∠1+∠3=90°∵DN⊥AD ∴∠2+∠3=90°∴∠1=∠2,∵DN⊥AD,AD∥BC ∴DN⊥BC ,又∵EM⊥AD ∴∠EMD=∠CND=90°又∵DC=DE ∴△DCN≌△DEM(AAS)∴ME=CN S△ADE=
 即3=
即3=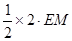 ,∴EM=CN=3 ∴BC=BN+CN=2+3=5
,∴EM=CN=3 ∴BC=BN+CN=2+3=5
练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
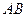 为
为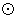
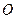 的直径,
的直径,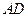 与
与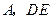 与
与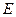 ,点
,点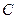 为
为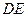 延长线上一点,且
延长线上一点,且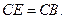
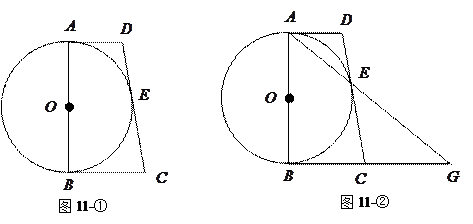
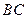 为
为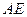 ,
,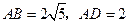 ,求线段
,求线段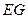 的长.
的长. 的矩形台球桌
的矩形台球桌 ,一球从点
,一球从点 (点
(点 上)
上)
 射向边
射向边 ,然后反弹到边
,然后反弹到边 上的
上的 点. 如果
点. 如果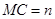 ,
, .那么
.那么 点的距离为 .
点的距离为 .

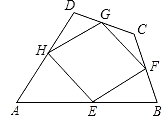


 = ,BF= .
= ,BF= .