题目内容
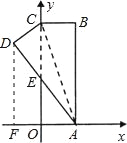
【题目】如图.在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.那么点D的坐标为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
(1)如图,过D作DF⊥AF于F,根据折叠可以证明△CDE≌△AOE,然后利用全等三角形的性质得到OE=DE,OA=CD=1,设OE=x,则CE=3﹣x,DE=x,利用勾股定理即可求出x;再利用已知条件可以证明△AEO∽△ADF,而AD=AB=3,根据相似三角形的性质即可求出DF、AF的长度,由此即可求出点D的坐标.
如图,过D作DF⊥AF于F,
∵点B的坐标为(1,3),
∴AO=1,AB=3,
根据折叠可知:CD=OA,
而∠D=∠AOE=90°,∠DEC=∠AEO,
∴△CDE≌△AOE,
∴OE=DE,OA=CD=1,
设OE=x,那么CE=3﹣x,DE=x,
∴在Rt△DCE中,CE2=DE2+CD2,
∴(3﹣x)2=x2+12,
∴x=![]() ,
,
又DF⊥AF,
∴DF∥EO,
∴△AEO∽△ADF,
而AD=AB=3,
∴AE=CE=3﹣![]() =
=![]() ,
,
∴![]() ,
,
即![]() ,
,
∴DF=![]() ,AF=
,AF=![]() ,
,
∴OF=![]() ﹣1=
﹣1=![]() ,
,
∴D的坐标为(﹣![]() ,
,![]() ).
).
故选A.

练习册系列答案
相关题目