题目内容
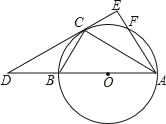
【题目】如图,已知△ABC内接于⊙O,AB是⊙O的直径,点F在⊙O上,且点C是![]() 的中点,过点C作⊙O的切线交AB的延长线于点D,交AF的延长线于点E.
的中点,过点C作⊙O的切线交AB的延长线于点D,交AF的延长线于点E.
(1)求证:AE⊥DE;
(2)若∠BAF=60°,AF=4,求CE的长.
【答案】(1)证明见解析;(2)![]()
【解析】
试题(1)首先连接OC,由OC=OA,![]() ,易证得OC∥AE,又由DE切⊙O于点C,易证得AE⊥DE;
,易证得OC∥AE,又由DE切⊙O于点C,易证得AE⊥DE;
(2)由AB是⊙O的直径,可得△ABC是直角三角形,易得△AEC为直角三角形,根据AE=3求得AC的长,然后连接OF,可得△OAF为等边三角形,知AF=OA=![]() AB,在△ACB中,利用已知条件求得答案.
AB,在△ACB中,利用已知条件求得答案.
试题解析:(1)证明:连接OC,
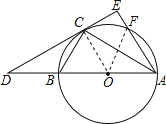
∵OC=OA,
∴∠BAC=∠OCA,
∵![]()
∴∠BAC=∠EAC,
∴∠EAC=∠OCA,
∴OC∥AE,
∵DE切⊙O于点C,
∴OC⊥DE,
∴AE⊥DE;
(2)解:∵AB是⊙O的直径,
∴△ABC是直角三角形,
∵∠CBA=60°,
∴∠BAC=∠EAC=30°,
∵△AEC为直角三角形,AE=3,
∴AC=2![]() ,
,
连接OF,
∵OF=OA,∠OAF=∠BAC+∠EAC=60°,
∴△OAF为等边三角形,
∴AF=OA=![]() AB,
AB,
在Rt△ACB中,AC=2![]() ,tan∠CBA=
,tan∠CBA=![]() ,
,
∴BC=2,
∴AB=4,
∴AF=2.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目