题目内容
【题目】如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120°.以点D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN.
(1)求证:MN=BM+NC;
(2)求△AMN的周长.

【答案】(1)证明见解析;(2)6.
【解析】
(1)先证明△BDF≌△CDN,得出∠BDF=∠CDN,DF=DN,同时再证明△DMN≌△DMF,得出MN=MF=MB+BF=MB+CN.
(2)根据MN=MB+CN,得出△AMN的周长为AM+AN+MN=AM+MB+AN+CN=AB+AC=6.
解:(1)∵△BDC是等腰三角形,且∠BDC=120°,∴∠BCD=∠DBC=30°.
∵△ABC是等边三角形,∴∠ABC=∠BCA=60°,
∴∠DBA=∠DCA=90°,
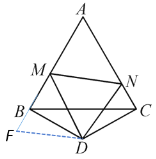
延长AB至F,使BF=CN,连接DF,
由SAS可证△BDF≌△CDN,
∴∠BDF=∠CDN,DF=DN,
∵∠MDN=60°,∴∠FDM=∠BDM+∠CDN=60°,
由SAS可证△DMN≌△DMF,
∴MN=MF=MB+BF=MB+CN
(2)由(1)知MN=MB+CN,
∴△AMN的周长为AM+AN+MN=AM+MB+AN+CN=AB+AC=6

【题目】(1)某校招聘教师一名,现有甲、乙、丙三人通过专业知识、讲课、答辩三项测试,他们各自的成绩如下表所示:
应聘者 | 专业知识 | 讲课 | 答辩 |
甲 | 70 | 85 | 80 |
乙 | 90 | 85 | 75 |
丙 | 80 | 90 | 85 |
按照招聘简章要求,对专业知识、讲课、答辩三项赋权5:4:1.请计算三名应聘者的平均成绩,从成绩看,应该录取谁?
(2)我市举行了某学科实验操作考试,有A、B、C、D四个实验,规定每位学生只参加其中一个实验的考试,并由学生自己抽签决定具体的考试实验.小王,小张,小厉都参加了本次考试.
①小厉参加实验D考试的概率是 ;
②用列表或画树状图的方法求小王、小张抽到同一个实验的概率.








