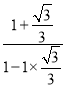题目内容
【题目】若等腰三角形一腰上的高是腰长的一半,则这个等腰三角形的底角是( )
A.75°或15°
B.75°
C.15°
D.75°或30°
【答案】A
【解析】解:当等腰三角形是锐角三角形时,如图1所示 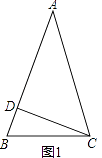
∵CD⊥AB,CD= ![]() AC,
AC,
∴sin∠A= ![]() =
= ![]() ,
,
∴∠A=30°,
∴∠B=∠ACB=75°;
当等腰三角形是钝角三角形时,如图2示,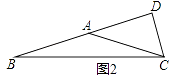
∵CD⊥AB,即在直角三角形ACD中,CD= ![]() AC,
AC,
∴∠CAD=30°,
∴∠CAB=150°,
∴∠B=∠ACB=15°.
故其底角为15°或75°.
故选A.
【考点精析】本题主要考查了等腰三角形的性质和含30度角的直角三角形的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半才能正确解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目