题目内容
【题目】如图所示,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC.∠EBC=∠E=60°,若BE=6,DE=2,则BC的长度是( ) 
A.6
B.8
C.9
D.10
【答案】B
【解析】解:延长ED交BC于M,延长AD交BC于N, ∵AB=AC,AD平分∠BAC,
∴AN⊥BC,BN=CN,
∵∠EBC=∠E=60°,
∴△BEM为等边三角形,
∴BE=EM
∵BE=6,DE=2,
∴DM=EM﹣DE═6﹣2=4,
∵△BEM为等边三角形,
∴∠EMB=60°,
∵AN⊥BC,
∴∠DNM=90°,
∴∠NDM=30°,
∴NM=2,
∴BN=4,
∴BC=2BN=8,
故选B.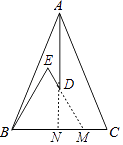
【考点精析】利用等腰三角形的性质对题目进行判断即可得到答案,需要熟知等腰三角形的两个底角相等(简称:等边对等角).

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目