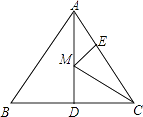题目内容
【题目】如图所示,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB交AB于E,F在AC上,∠B=∠CFD. 证明:
(1)CF=EB
(2)AB=AF+2EB.
【答案】
(1)证明:∵AD是∠BAC的平分线,
∴∠CAD=∠DAE,
由已知有:∠ADC=90°﹣∠CAD,∠ADE=90°﹣∠DAE,
∴∠ADC=∠ADE,
在△ACD和△AED中
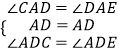
∴△ACD≌△AED(ASA),
∴CF=EB
(2)
证明:由(1)知FC=EB,AC=AE,
∴AB=AE+EB=AC+EB=AF+FC+EB=AF+2EB
【解析】(1)证明△ACD≌△AED即可;(2)由AB=AE+BE,结合条件可知AE=AC且BE=CF,代入可证得结论.
【考点精析】本题主要考查了角平分线的性质定理的相关知识点,需要掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上才能正确解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目