题目内容
【题目】如图,在Rt△ABC中,∠B=90°,直线EF分别交两直角边AB、BC与E、F两点,且EF∥AC,P是斜边AC的中点,连接PE,PF,且AB= ![]() ,BC=
,BC= ![]() .
.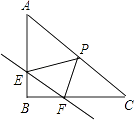
(1)当E、F均为两直角边的中点时,求证:四边形EPFB是矩形,并求出此时EF的长;
(2)设EF的长度为x(x>0),当∠EPF=∠A时,用含x的代数式表示EP的长;
(3)设△PEF的面积为S,则当EF为多少时,S有最大值,并求出该最大值.
【答案】
(1)
解:如图1,
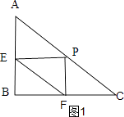
∵E是AB的中点,P是AC的中点,
∴EP∥BC,且EP= ![]() BC,
BC,
∵F是BC的中点,
∴EP∥BF,且EP=BF,
四边形EPFB是平行四边形,
∵∠B=90°,
∴四边形EPFB是矩形
(2)
解:∵AB= ![]() ,BC=
,BC= ![]() .
.
∴BE= ![]() ,BF=
,BF= ![]() ,
,
∴EF= ![]() =1.(2)∵EF∥AC,
=1.(2)∵EF∥AC,
∴∠APE=∠PEF,∵∠EPF=∠A,
∴△APE∽△PEF.
∴ ![]() ,
,
∵AP=1,EF=x,
∴EP2=x,
∴EP= ![]()
(3)
解:如图2,作FH⊥AC交AC于点H,
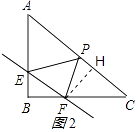
∵EF∥AC,
∴△BEF∽△BAC,
设EF=x,则BF= ![]() x,CF=
x,CF= ![]() ﹣
﹣ ![]() x,
x,
∴FH= ![]() CF=
CF= ![]() ﹣
﹣ ![]() x,
x,
∴S= ![]() EFFH=﹣
EFFH=﹣ ![]() x2+
x2+ ![]() x=﹣
x=﹣ ![]() (x﹣1)2+
(x﹣1)2+ ![]() ,
,
∴当x=1,即EF=1时,S有最大值为 ![]() .
.
【解析】(1)先求出四边形EPFB是平行四边形,再由∠B=90°得出四边形EPFB是矩形,利用勾股定理求出EF.(2)证明△APE∽△PEF,得出对应边成比例,即可得出结果.(3)作FH⊥AC交AC于点H,设EF=x,得出BF,CF及FH的值,再利用三角形面积求出EF及最大值,利用中位线定理即可求出EP的值.

 优生乐园系列答案
优生乐园系列答案【题目】在读书月活动中,某校号召全体师生积极捐书,为了解所捐书籍的种类,图书管理员对部分书籍进行了抽样调查,根据调查数据绘制了如下不完整的统计图表.请你根据统计图表所提供的信息回答下面问题:
某校师生捐书种类情况统计表
种类 | 频数 | 百分比 |
A.科普类 | 12 | n |
B.文学类 | 14 | 35% |
C.艺术类 | m | 20% |
D.其它类 | 6 | 15% |
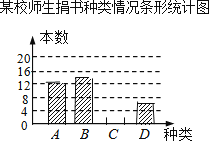
(1)统计表中的m= , n=;
(2)补全条形统计图;
(3)本次活动师生共捐书2000本,请估计有多少本科普类图书?
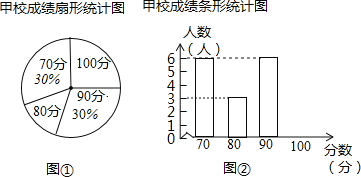
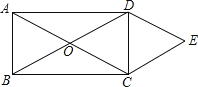
【题目】某市团委举行以“我的中国梦”为主题的知识竞赛,甲、乙两所学校的参赛人数相等,比赛结束后,发现学生成绩分别为70分,80分,90分,100分,并根据统计数据绘制了如图不完整的统计图表:
乙校成绩统计表 | |
分数 | 人数 |
70 | 7 |
80 | ______ |
90 | 1 |
100 | 8 |
![]() 乙学校的参赛人数是______人
乙学校的参赛人数是______人![]()
![]() 在图
在图![]() 中,“80分”所在扇形的圆心角度数为______;
中,“80分”所在扇形的圆心角度数为______;
![]() 请你将图
请你将图![]() 补充完整;
补充完整;
![]() 求乙校成绩的平均分.
求乙校成绩的平均分.