题目内容
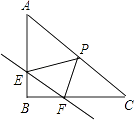
【题目】如图,在平面直角坐标系中,点O为坐标原点,直线l分别交x轴、y轴于A、B两点,AB=5,OA:OB =3:4.
(1)求直线l的表达式;
(2)点P是![]() 轴上的点,点Q是第一象限内的点.若以A、B、P、Q为顶点的四边形是菱形,请直接写出Q点的坐标.
轴上的点,点Q是第一象限内的点.若以A、B、P、Q为顶点的四边形是菱形,请直接写出Q点的坐标.

【答案】(1)y=![]() +4 (2)(3,5)或(3,
+4 (2)(3,5)或(3,![]() )
)
【解析】
(1)首先根据已知条件以及勾股定理求得OA、OB的长度,即求得A、B的坐标,利用待定系数法即可求解;
(2)分P在B点的上边和在B的下边两种情况画出图形进行讨论,求得Q的坐标.
(1)∵OA:OB=3:4,AB=5,
∴根据勾股定理,得OA=3,OB=4,
∵点A、B在x轴、y轴上,
∴A(3,0),B(0,4),
设直线l表达式为y=kx+b(k≠0),
∵直线l过点A(3,0),点B(0,4),
∴![]() ,
,
解得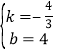 ,
,
∴直线l的表达式为y=![]() +4;
+4;
(2)如图,当四边形BP1AQ1是菱形时,则有BP1=AP1=AQ1,
则有OP1=4-BP1,
在Rt△AOP1中,有AP12=OP12+AO2,
即AQ12=(4-AQ1)2+32,
解得:AQ1=![]() ,所以Q1的坐标为(3,
,所以Q1的坐标为(3,![]() );
);
当四边形BP2Q2A是菱形时,则有BP2 =AQ2=AB=5,
所以Q2的坐标为(3,5),
综上所述,Q点的坐标是(3,5)或(3,).

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目