ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮOABCЕФЖЅЕуOдкзјБъдЕуЃЌЖЅЕуAЕФзјБъЮЊ(4ЃЌ3)ЃЎ
(1)ЖЅЕу![]() ЕФзјБъЮЊ( ЃЌ )ЃЛ
ЕФзјБъЮЊ( ЃЌ )ЃЛ
(2)ЯжгаЖЏЕуPЁЂQЗжБ№ДгCЁЂAЭЌЪБГіЗЂЃЌЕуPбиЯпЖЮCBЯђжеЕуBдЫЖЏЃЌЫйЖШЮЊУПУы1ИіЕЅЮЛЃЌЕуQбиелЯпAЁњOЁњCЯђжеЕуCдЫЖЏЃЌЫйЖШЮЊУПУыkИіЕЅЮЛЃЌЕБдЫЖЏЪБМфЮЊ2УыЪБЃЌвдPЁЂQЁЂCЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЃЌЧѓДЫЪБkЕФжЕЃЎ
(3)Шєе§ЗНаЮOABCвдУПУы![]() ИіЕЅЮЛЕФЫйЖШбиЩфЯпAOЯТЛЌЃЌжБжСЖЅЕуCТфЕН
ИіЕЅЮЛЕФЫйЖШбиЩфЯпAOЯТЛЌЃЌжБжСЖЅЕуCТфЕН![]() жсЩЯЪБЭЃжЙЯТ
жсЩЯЪБЭЃжЙЯТ
ЛЌЃЎЩше§ЗНаЮOABCдк![]() жсЯТЗНВПЗжЕФУцЛ§ЮЊSЃЌЧѓSЙигкЛЌааЪБМф
жсЯТЗНВПЗжЕФУцЛ§ЮЊSЃЌЧѓSЙигкЛЌааЪБМф![]() ЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіЯргІздБфСП
ЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіЯргІздБфСП![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ


(БИгУЭМ)
ЁОД№АИЁП(1)C(Ѓ3ЃЌ4)(2) kЕФжЕЮЊ2Лђ4(3)Ђй![]() Ђк
Ђк![]() ЃЈ3ЃМtЁм4ЃЉ
ЃЈ3ЃМtЁм4ЃЉ
ЁОНтЮіЁПЗжЮіЃКЃЈ1ЃЉШчЭМ1жаЃЌзї![]() жсгк
жсгк![]() ЃЌ
ЃЌ![]() жсгкNЃЎвзжЄ
жсгкNЃЎвзжЄ![]() Ёе
Ёе![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЭЦГі
ЭЦГі![]()
ЃЈ2ЃЉЗжСНжжЧщаЮЂйЕБЕуQдкOAЩЯЪБЃЎЂкЕБЕуQдкOCЩЯЪБЃЎЗжБ№МЦЫуМДПЩЃЎ
ЃЈ3ЃЉЗжСНжжЧщаЮЂйЕБЕуAдЫЖЏЕНЕуOЪБЃЌt=3ЃЌЕБ0<tЁм3ЪБЃЌЩш![]() НЛxжсгкЕуEЃЌзї
НЛxжсгкЕуEЃЌзї![]() жсгкЕуFЃЈШчЭМ3жаЃЉЃЎЂкЕБЕуCдЫЖЏЕНxжсЩЯЪБЃЌt=4ЕБ3<tЁм4ЪБЃЈШчЭМ4жаЃЉЃЌЩш
жсгкЕуFЃЈШчЭМ3жаЃЉЃЎЂкЕБЕуCдЫЖЏЕНxжсЩЯЪБЃЌt=4ЕБ3<tЁм4ЪБЃЈШчЭМ4жаЃЉЃЌЩш![]() НЛxжсгкЕуFЃЎЗжБ№ЧѓНтМДПЩЃЎ
НЛxжсгкЕуFЃЎЗжБ№ЧѓНтМДПЩЃЎ
ЯъНтЃК(1)ШчЭМ1жаЃЌзїCMЁЭxжсгкЃЌANЁЭxжсгкN.
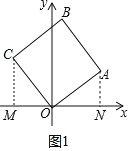
взжЄЁїAONЁеЁїCOMЃЌПЩЕУCM=ON=4ЃЌOM=AN=3ЃЌ
Ёр![]()
(2)гЩЬтвтЕУЃЌAO=CO=BC=AB=5ЃЌ
ЕБt=2ЪБЃЌCP=2.
ЂйЕБЕуQдкOAЩЯЪБЃЌ![]() ЃЌ
ЃЌ
ЁржЛДцдквЛЕуQЃЌЪЙQC=QP.
зїQDЁЭPCгкЕуD(ШчЭМ2жа)ЃЌдђCD=PD=1ЃЌ
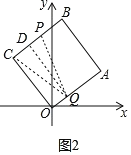
ЁрQA=2k=51=4ЃЌ
Ёрk=2.
ЂкЕБЕуQдкOCЩЯЪБ,гЩгкЁЯC=90ЫљвджЛДцдквЛЕуQЃЌЪЙCP=CQ=2ЃЌ
Ёр2k=102=8ЃЌЁрk=4.
злЩЯЫљЪіЃЌkЕФжЕЮЊ2Лђ4.
(3)ЂйЕБЕуAдЫЖЏЕНЕуOЪБЃЌt=3.
ЕБ![]() ЪБ,ЩшOЁЏCЁЏНЛxжсЕуE,зїAЁЏFЁЭxжсгкЕуF(ШчЭМ3жа).
ЪБ,ЩшOЁЏCЁЏНЛxжсЕуE,зїAЁЏFЁЭxжсгкЕуF(ШчЭМ3жа).
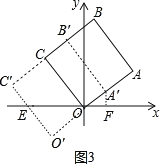
дђЁїAЁЏOFЁзЁїEOOЁЏЃЌ
ЁрЁр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() .
.
![]() .(
.(![]() ).
).
ЂкЕБЕуCдЫЖЏЕНxжсЩЯЪБЃЌt=4
ЕБ![]() ЪБ(ШчЭМ4жа)ЃЌЩшAЁЏBЁЏНЛxжсгкЕуFЃЌ
ЪБ(ШчЭМ4жа)ЃЌЩшAЁЏBЁЏНЛxжсгкЕуFЃЌ
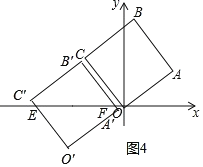
дђдђAЁЏO=![]() ЃЌ
ЃЌ
Ёр![]() .
.
Ёр![]() .(
.(![]() ).
).
злЩЯЫљЪі,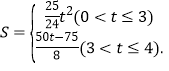

 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ