题目内容
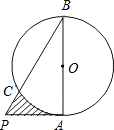
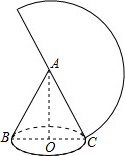
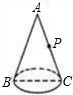
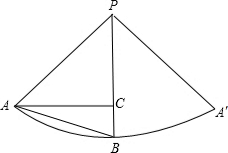
已知圆锥的底面半径为3cm，母线长为9cm，C为母线PB的中点，在圆锥的侧面上，从A到C的最短距离是______．
：圆锥的底面周长是6π，则6π=
，
∴n=120°，
即圆锥侧面展开图的圆心角是120°，
∴∠APB=60°，
∵PA=PB，
∴△PAB是等边三角形，
∵C是PB中点，
∴AC⊥PB，
∴∠ACP=90°，
∵在圆锥侧面展开图中AP=9，PC=4.5，
∴在圆锥侧面展开图中AC=
=
最短距离是
cm．
故答案为：
cm．
| nπ×9 |
| 180 |
∴n=120°，
即圆锥侧面展开图的圆心角是120°，
∴∠APB=60°，
∵PA=PB，
∴△PAB是等边三角形，
∵C是PB中点，
∴AC⊥PB，
∴∠ACP=90°，
∵在圆锥侧面展开图中AP=9，PC=4.5，
∴在圆锥侧面展开图中AC=
| AP2-PC2 |
9
| ||
| 2 |
最短距离是
9
| ||
| 2 |
故答案为：
9
| ||
| 2 |
练习册系列答案
浙江名校名师金卷系列答案
相关题目
