题目内容
如图,底面半径为5dm的圆柱形油桶横放在水平地面上,向桶内加油后,量得长方形油面的宽度为8dm,则油的深度(油面到水平地面的距离)为______dm.
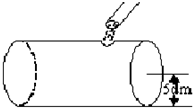

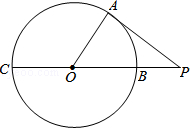
如图,已知OA=5dm,AB=8dm,OC⊥AB于D,求CD的长,
理由如下:当油面位于AB的位置时
∵OC⊥AB根据垂径定理可得,∴AD=4dm,
在直角三角形OAD中,
根据勾股定理可得OD=3dm,
所以CD=5-3=2(dm);
当油面位于A'B'的位置时,CD=5+3=8(dm).
故答案为:2或8.
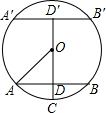
理由如下:当油面位于AB的位置时
∵OC⊥AB根据垂径定理可得,∴AD=4dm,
在直角三角形OAD中,
根据勾股定理可得OD=3dm,
所以CD=5-3=2(dm);
当油面位于A'B'的位置时,CD=5+3=8(dm).
故答案为:2或8.


练习册系列答案
相关题目