题目内容
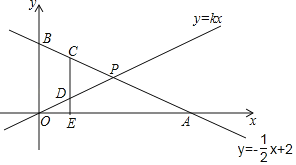
【题目】在平面直角坐标系中,一次函数y=﹣![]() x+2的图象交x轴、y轴分别于A、B两点,交直线y=kx于P.
x+2的图象交x轴、y轴分别于A、B两点,交直线y=kx于P.
(1)求点A、B的坐标;
(2)若OP=PA,求k的值;
(3)在(2)的条件下,C是线段BP上一点,CE⊥x轴于E,交OP于D,若CD=2ED,求C点的坐标.
【答案】(1)点A的坐标为(4,0),点B的坐标为(0,2);(2)k=![]() ;(3)点C的坐标为(1,
;(3)点C的坐标为(1,![]() ).
).
【解析】
(1)分别令![]() 和
和![]() 求解即可得;
求解即可得;
(2)先根据等腰三角形的性质可求出点P的横坐标,再根据![]() 可求出点P的坐标,然后代入
可求出点P的坐标,然后代入![]() 即可得;
即可得;
(3)设点C的坐标为![]() ,从而可得点D的坐标,再根据“
,从而可得点D的坐标,再根据“![]() ”列出方程求解即可得.
”列出方程求解即可得.
(1)对于![]()
当![]() 时,
时,![]() ,则点B的坐标为
,则点B的坐标为![]()
当![]() 时,
时,![]() ,解得
,解得![]() ,则点A的坐标为
,则点A的坐标为![]() ;
;
(2)∵![]()
∴![]() 是等腰三角形
是等腰三角形
![]()
![]()
![]() 点P的横坐标为
点P的横坐标为![]()
当![]() 时,
时,![]()
∴点P的坐标为![]()
∵点P在直线![]() 上
上
∴![]()
解得![]() ;
;
(3)设点C的坐标为![]()
![]() ,则点D的坐标为
,则点D的坐标为![]() ,点E的坐标为
,点E的坐标为![]()
∴![]() ,
,![]()
∵![]()
∴![]()
解得![]()
则![]()
故点C的坐标为![]() .
.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目