题目内容
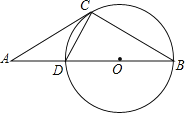
【题目】如图,已知直线AC与⊙O相交于点C,直线AO与⊙O相交于D,B两点.已知∠ACD=∠B.
(1)求证:AC是⊙O的切线;
(2)若AC=6,AD=4,求⊙O的半径;
【答案】(1)证明见解析;(2)![]()
【解析】
连接OC,利用圆周角定理及等腰三角形的性质得出∠OCA=90°,进而得出答案.
易知△ACD∽△ABC,则![]() =
=![]() ,又AB=4+DB,即可求出DB,得到半径.
,又AB=4+DB,即可求出DB,得到半径.
(1)连接OC,
∵OC=OB,
∴∠BCO=∠B,
∵DB是⊙O直径,
∴∠DCB=90°,
∴∠DCO+∠BCO=∠DCO+∠B=90°,
∵∠ACD=∠B.
∴∠DCO+∠ACD=∠ACO=90°,
∴AC是⊙O的切线.
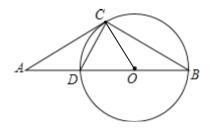
(2)∵∠ACD=∠B.
∵∠A=∠A.
∴△ACD∽△ABC
∴AC2 =AD×AB
∴62=4×(4+DB)
∴DB=5.
∴⊙O的半径是![]() .
.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目