题目内容
【题目】已知⊙O中,AC为直径,MA、MB分别切⊙O于点A、B.
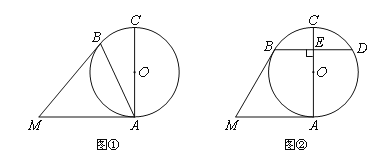
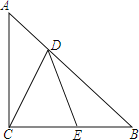
(Ⅰ)如图①,若∠BAC=250,求∠AMB的大小;
(Ⅱ)如图②,过点B作BD⊥AC于点E,交⊙O于点D,若BD=MA,求∠AMB的大小.
【答案】(Ⅰ)50°(Ⅱ)60°
【解析】解:(Ⅰ)∵MA切⊙O于点A,∴∠MAC=90°。
又∠BAC=25°,∴∠MAB=∠MAC-∠BAC=65°。
∵MA、MB分别切⊙O于点A、B,∴MA=MB。
∴∠MAB=∠MBA。
∴∠AMB=180°-(∠MAB+∠MBA)=50°。
(Ⅱ)如图,连接AD、AB,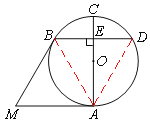
∵MA⊥AC,又BD⊥AC,
∴BD∥MA。
又∵BD=MA,∴四边形MADB是平行四边形。
又∵MA=MB,∴四边形MADB是菱形。∴AD=BD。
又∵AC为直径,AC⊥BD,
∴ AB = AD 。
∴AB=AD=BD。∴△ABD是等边三角形。∴∠D=60°。
∴在菱形MADB中,∠AMB=∠D=60°
(Ⅰ)由AM与圆O相切,根据切线的性质得到AM垂直于AC,可得出∠MAC为直角,再由∠BAC的度数,用∠MAC-∠BAC求出∠MAB的度数,又MA,MB为圆O的切线,根据切线长定理得到MA=MB,利用等边对等角可得出∠MAB=∠MBA,由底角的度数,利用三角形的内角和定理即可求出∠AMB的度数。
(Ⅱ)连接AB,AD,由直径AC垂直于弦BD,根据垂径定理得到A为优弧BAD 的中点,根据等弧对等弦可得出AB=AD,由AM为圆O的切线,得到AM垂直于AC,又BD垂直于AC,根据垂直于同一条直线的两直线平行可得出BD平行于AM,又BD=AM,利用一组对边平行且相等的四边形为平行四边形得到ADBM为平行四边形,再由邻边MA=MB,得到ADBM为菱形,根据菱形的邻边相等可得出BD=AD,进而得到AB=AD=BD,即△ABD为等边三角形,根据等边三角形的性质得到∠D为60°,再利用菱形的对角相等可得出∠AMB=∠D=60°。

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案