题目内容
【题目】如图,在菱形 ABCD 中,B 60 ,M 、N 分别为线段 AB 、BC 上的两点,且 BM CN , AN 、CM 相交于点 E 。
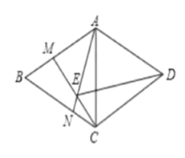
(1)证明: BCM ≌ CAN 。
(2)求AEM 的度数。
(3)证明: AE CE DE 。
【答案】(1)见解析;(2)60°; (3)见解析.
【解析】
(1)由题意可得△ABC,△ADC都是等边三角形,根据SAS即可证明△BCM≌△CAN.
(2)由△BCM≌△CAN,推出∠BCM=∠CAN,推出∠AEM=∠ACE+∠EAC=∠ACE+∠BCM=60°,作DG⊥AN于G,DH⊥MC交MC的延长线于H,由△DGA≌△DHC,推出DG=DH,由DG⊥AN,DH⊥MC,推出∠DEG=∠DEH,即可得到∠AED的度数.
(3)由(2)可知,∠GED=60°,在Rt△DEG中,由∠EDG =30°,推出DE=2EG,易证△DEG≌△DEH,推出EG=EH,推出EA+EC=EG+AG+EH-CH,由△DGA≌△DHC,推出GA=CH,推出EA+EC=2EG=DE.
解:(1)∵四边形ABCD是菱形,
∴AB=BC=CD=AD,
∵∠B=60°,
∴△ACD,△ABC是等边三角形,
∴BC=AC,∠B=∠ACN=60°,
在△BCM和△CAN中,
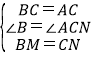 ,
,
∴△BCM≌△CAN(SAS).
(2)∵△BCM≌△CAN,
∴∠BCM=∠CAN,
∴∠AEM=∠ACE+∠EAC=∠ACE+∠BCM=60°,
如图,作DG⊥AN于G,DH⊥MC,交MC的延长线于H,

∵∠AEM=60°,
∴∠AEC=120°,
∵∠DGE=∠H=90°,
∴∠GEH+∠GDH=180°,
∴∠GDH=∠ADC=60°,
∴∠ADG=∠CDH,
在△DGA和△DHC中,
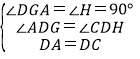 ,
,
∴△DGA≌△DHC(AAS),
∴DG=DH,
∵DG⊥AN,DH⊥MC,
∴∠DEG=∠DEH,
∴DE平分∠AEC,即∠AED=60°.
(3)证明:由(2)可知,∠GED=60°,
在Rt△DEG中,∵∠EDG=30°,
∴DE=2EG,
在△DEG和△DEH中,
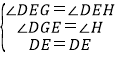 ,
,
∴△DEG≌△DEH(AAS),
∴EG=EH,
∵△DGA≌△DHC,
∴GA=CH,
∴EA+EC=EG+AG+EH-CH=2EG=DE.即EA+EC=ED.

 阅读快车系列答案
阅读快车系列答案【题目】某校为了调查学生书写规范汉字的能力,从七年级1000名学生中随机抽选了部分学生参加测试,并根据测试成绩绘制了如下频数分布表和扇形统计图(尚不完整)
组别 | 成绩x分 | 频数(人数) |
第1组 | x<60 | 4 |
第2组 | 60≤x<70 | a |
第3组 | 70≤x<80 | 20 |
第4组 | 80≤x<90 | b |
第5组 | 90≤x<100 | 10 |

请结合图表完成下列各题
(1)填空:表中a的值为_______,b的值为_______,扇形统计图中表示第1组所对应的圆心角度数为_______.
(2)若测试成绩不低于80分为优秀,请你估计从该校七年级学生中随机抽查一个学生,他是规范汉字书写优秀的概率是_______;
(3)若测试成绩在60~80分之间(含60分,不含80分)为合格,请你估计则该校七年级学生规范汉字书写不合格的人数.
【题目】“十·一”黄金周期间,武汉动物园在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
人数变化单位:万人 | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(1)若9月30日的游客人数记为![]() ,请用
,请用![]() 的代数式表示10月2日的游客人数?
的代数式表示10月2日的游客人数?
(2)请判断七天内游客人数最多的是哪天?请说明理由。
(3)若9月30日的游客人数为2万人,门票每人10元。问黄金周期间武汉动物园门票收入是多少元?