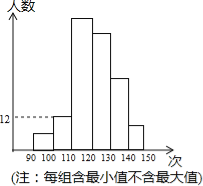
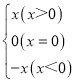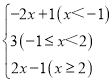��Ŀ����
����Ŀ����֪��b����С������������a��b����![]() ����ش����⣺
����ش����⣺
��1����ֱ��д��a��b��c��ֵ�� a=______�� b=________�� c=________��
��2��a��b��c����Ӧ�ĵ�ֱ�ΪA��B��C������B���C֮��ľ����ʾΪBC����A���B֮��ľ����ʾΪAB���Լ����ʱBC��AB��ֵ��
![]()
��3���ڣ�1����2���������£���A��B��C��ʼ���������˶�������A��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ����B�͵�C�ֱ���ÿ��3����λ���Ⱥ�x��x>3������λ���ȵ��ٶ������˶������ʣ��Ƿ����x��ʹBC��AB��ֵ����ʱ��t�ı仯�����䣬���������x����������˵�����ɣ�
���𰸡�(1)a=-1��b=1��c=4�� (2)1�� (3)x=7
��������
��1������b����С��������������ȷ��b��ֵ��Ȼ����ݷǸ��������ʣ������Ǹ����ĺ���0����ÿ������0���������a��b��c��ֵ��
��2�����������ľ��빫ʽ����BC��AB��ֵ����һ���õ�BC-AB��ֵ��
��3�������BC=4t+3��AB=4t+2���Ӷ��ó�BC-AB���Ӷ���⣮
�⣺��1����b����С����������
��b=1��
��|c-4|+��a+b��2=0��
��c-4=0��a+b=0����a=-1��c=4��
��2��BC-AB
=��4-1��-��1+1��
=3-2
=1��
�ʴ�ʱBC-AB��ֵ��1��
��3��t��ʱ����A��Ӧ����Ϊ-1-t����B��Ӧ����Ϊ3t+1����C��Ӧ����Ϊxt+4��
��BC=��xt+4��-��3t+1��=(x-3)t+3��AB=��3t+1��-��-1-t��=4t+2��
��BC-AB=(x-3)t+3-��4t+2��=��x-7��t+1��
��BC-AB��ֵ������ʱ��t�ı仯���ı�ʱ����ֵΪ7��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�