题目内容
【题目】如图,已知 AD 与 BC 相交于 E ,1 2 3, BD CD, ADB 90, CH AB于 H , CH 交 AD 于 F 。
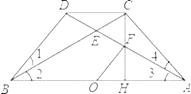
(1)求证: CD∥ AB ;
(2)求证: BDE ≌ ACE ;
(3)若O 为 AB 中点,求证:OF=![]() BE 。
BE 。
【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】
(1)有BD=CD,可得∠1=∠BCD,那么就有∠2=∠BCD,从而CD∥AB;
(2)由∠2=∠3,可得BE=AE,又因为CD∥AB,同样可知DE=CE,根据SAS即可证出:△BDE≌△ACE;
(3)由于O是AB的中点,因此只需证得AF=EF即可得出OF是△ABE的中位线,进而可得出OF=![]() BE.根据(2)的全等三角形,可得出∠ACE=90°,因此可通过证CF是直角三角形ACE斜边上的中线,来得出AF=EF.
BE.根据(2)的全等三角形,可得出∠ACE=90°,因此可通过证CF是直角三角形ACE斜边上的中线,来得出AF=EF.
证明:(1)∵BD=CD,
∴∠BCD=∠1;
∵∠1=∠2,
∴∠BCD=∠2;
∴CD∥AB.
(2)∵CD∥AB,
∴∠CDA=∠3.
∵∠BCD=∠2=∠3,
∴BE=AE,且∠CDA=∠BCD,
∴DE=CE.
在△BDE和△ACE中,
 ,
,
∴△BDE≌△ACE(SAS);
(3)∵△BDE≌△ACE,
∴∠4=∠1,∠ACE=∠BDE=90°,
∴∠ACH=90°-∠BCH;
又∵CH⊥AB,
∴∠2=90°-∠BCH;
∴∠ACH=∠2=∠1=∠4,
∴AF=CF;
∵∠AEC=90°-∠4,∠ECF=90°-∠ACH,
又∵∠ACH=∠4,
∴∠AEC=∠ECF;
∴CF=EF;
∴EF=AF;
∵O为AB中点,
∴OF为△ABE的中位线,
∴OF=![]() BE.
BE.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】八年 2 班组织了一次经典诵读比赛,甲乙两组各 10 人的比赛成绩如下表(10 分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(Ⅰ)甲组数据的中位数是 ,乙组数据的众数是 ;
(Ⅱ)计算乙组数据的平均数和方差;
(Ⅲ)已知甲组数据的方差是 1.4 分,则成绩较为整齐的是 。