题目内容
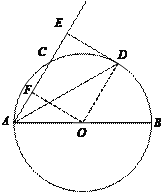
【题目】如图,AB是⊙O的直径,AC与⊙O交于点C,∠BAC的平分线交⊙O于点D,DE⊥AC,垂足为E.
(1)求证:DE是⊙O的切线;
(2)若直径AB=10,弦AC=6,求DE的长.

【答案】(1)见解析;(2)4.
【解析】试题分析: ![]() 连结OD,∵AD平分∠BAC,∠OAD=∠CAD,∵OA=OD,
连结OD,∵AD平分∠BAC,∠OAD=∠CAD,∵OA=OD,
∴∠OAD=∠ODA,∴∠ODA=∠CAD,得出OD∥AC,得到∠ODE=90°,从而得证.
![]() 在Rt△AFO中,利用勾股定理:AF2+OF2=AO2,得出
在Rt△AFO中,利用勾股定理:AF2+OF2=AO2,得出![]() 的长,四边形ODEF是矩形,从而得到
的长,四边形ODEF是矩形,从而得到![]() 的长.
的长.
试题解析: ![]() 连结OD.
连结OD.
∵AD平分∠BAC,
∴∠OAD=∠CAD,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠ODA=∠CAD,
∴OD∥AC,
∵DE⊥AC,
即∠AED=90°,
∴∠ODE=90°,
即DE⊥OD.
∴DE是⊙O的切线.
(2)解:作OF⊥AC,垂足为F.
![]()
在Rt△AFO中,AF2+OF2=AO2, ![]()
∴32+OF2=52,
∴ OF=4,
∵∠AED=∠ODE=∠OFE=90°,
∴四边形ODEF是矩形,
∴DE=OF=4.

【题目】为了让学生了解“阳光体育”知识,我市某中学举行了一次“阳光体育”知识竞赛,共有1800名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面的频数分布表和频数分布直方图,解答下列问题:
频数分布直方图 频数分布表
分组 | 频数 | 频率 |
50.5~60.5 | 4 | 0.08 |
60.5~70.5 | 8 | 0.16 |
70.5~80.5 | 12 | 0.24 |
80.5~90.5 | 15 | 0.30 |
90.5~100.5 | a | b |
合计 |

(1)频数分布表中a=_________,b=__________;
(2)补全频数分布直方图;
(3)若成绩在80分以上(不含80分)为优秀,则该校成绩没达到优秀的约为多少人?


