Question

【题目】如图，抛物线与轴交于A、B两点（点A在点B的左侧），与轴交于点C。连接BC,AC，△ABC的外接圆记为⊙M, 点D是⊙M与轴的另一个交点。

（1）求出点A，B，C的坐标；

（2）求证：弧AD=弧BC

（3）求⊙M的半径；

（4）如图，点P为⊙M上的一个动点，问：当点P的坐标是多少时，以A,B,C,P为顶点的四边形有最大面积，并求其最大面积。

Answer 1

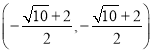【答案】(1) A(-3，0),B(1，0)，C(0,-3)；（2）证明见解析；（3）；（4）P的坐标是；最大面积是.

【解析】试题分析：（1）在y=x2+2x-3中令y=0，解方程求得x即可求得A和B的横坐标，在y=x2+2x-3中令x=0求得C的纵坐标；

（2）根据（1）可得AB=CD，然后根据同圆中，弦相等，则对应的弧相等，从而证得；
（3）易证△MBC是等腰直角三角形，利用三角函数即可求解；

（4）当P在弧AC上，且到AC的距离最远，即是AC弧的中点时，四边形的面积最大，求得P的坐标，即可求得四边形的面积．

解（1）当=0时， =-3

∴C(0,-3)

当=0时，

解得：

∴A(-3，0),B(1，0)

（2）∵A(-3，0), C(-3，0)

∴OA=OC

∵

∴∠OAC=∠OCA=45°

∴

（3）∵∠OAC =45°

∴∠CMB=90°

连接MC，MB,在等腰直角三角形MBC中，BC=

∴r=

（4）P的坐标是

最大面积是.