题目内容
【题目】观察以下等式：
第1个等式：23-22=13＋2×1＋1；
第2个等式：33-32=23＋3×2＋22；
第3个等式：43-42=33＋4×3＋32；
……
按照以上规律，解决下列问题：
（1）写出第4个等式：__________________；
（2）写出你猜想的第n个等式（用含n的等式表示），并证明．
【答案】（1）
；（2）猜想出第
个等式为
，证明见解析．
【解析】
（1）根据前三个等式归纳总结出规律即可得；
（2）先归纳总结出一般规律，得出第n个等式，再利用因式分解的方法分别计算等式的两边即可得证．
（1）由前三个等式可得：第4个等式为
故答案为：；
（2）猜想出第个等式为，证明如下：
等式的左边
等式的右边
则等式的左边
等式的右边
所以等式成立．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
【题目】今年疫情防控期间，我市一家服装有限公司生产了一款服装，为对比分析以前实体商店和现在网上商店两种途径的销售情况，进行了为期30天的跟踪调查．其中实体商店的日销售量
（百件）与时间
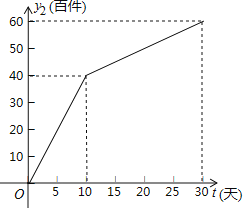
（为整数，单位：天）的部分对应值如下表所示；网上商店的日销售量
（百件）与时间（为整数，单位：天）的关系如图所示．
时间 | 0 | 6 | 10 | 12 | 18 | 20 | 24 | 30 |
日销售量 | 0 | 72 | 100 | 108 | 108 | 100 | 72 | 0 |
（1）请你在一次函数、二次函数和反比例函数中，选择合适的函数反映与的变化规律，并求出与的函数关系式及自变量的取值范围；
（2）求与的函数关系式，并写出自变量的取值范围；
（3）在跟踪调查的30天中，设实体商店和网上商店的日销售总量为
（百件），求与的函数关系式；当为何值时，日销售量达到最大，并求出此时的最大值．
