题目内容
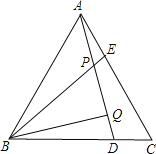
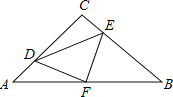
【题目】如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持AD=CE.连接DE、DF、EF.在此运动变化的过程中,下列结论:①△DFE是等腰直角三角形;②DE长度的最小值为4;③四边形CDFE的面积保持不变;④△CDE面积的最大值为8.其中正确的结论是( )
A.①②③B.①③C.①③④D.②③④
【答案】C
【解析】
①连接CF,构造全等三角形,证明△ADF≌△CEF即可.
②通过①可得△DFE是等腰直角三角形,则斜边DE=![]() DF,求得DF的最小值即可得到DE的最小值.
DF,求得DF的最小值即可得到DE的最小值.
③通过证明△ADF≌△CEF,进行等面积代换即可得出.
④通过结论③,换角度将四边形CDFE的面积分为△CDE与△DEF,令△DEF的面积最小即可.
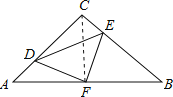
①连接CF.
∵△ABC为等腰直角三角形,
∴∠FCB=∠A=45°,CF=AF=FB,
∵AD=CE,
∴△ADF≌△CEF,
∴EF=DF,∠CFE=∠AFD,
∵∠AFD+∠CFD=90°
∴∠CFE+∠CFD=∠EFD=90°,
∴△EDF是等腰直角三角形,
故本选项正确;
②∵△DEF是等腰直角三角形,
∴当DE最小时,DF也最小,
即当DF⊥AC时,DE最小,此时DF=![]() BC=4,
BC=4,
∴DE=![]() DF=
DF=![]() ,
,
故本选项错误;
③∵△ADF≌△CEF,
∴S△CEF=S△ADF,
∴S四边形CDFE=S△DCF+S△CEF=S△DCF+S△ADF=S△ACF=![]() S△ABC
S△ABC
故本选项正确;
④当△CED面积最大时,由③知,此时△DEF的面积最小,此时,
S△CED=S四边形CEFD﹣S△DEF=S△AFC﹣S△DEF=16﹣8=8,
故本选项正确;
综上所述正确的有①③④.
故选:C.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目