题目内容
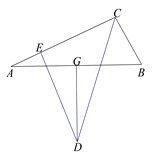
【题目】如图,![]() 中,
中,![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 的平分线
的平分线![]() 于点
于点![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
连接BD、AD,过点D作DF⊥CB于点F,利用角平分线及线段垂直平分线的性质可求出BD=AD,DE=DF,依据HL定理可判断出Rt△AED≌Rt△BFD,根据全等三角形的性质即可得出BF=AE,再运用AAS定理可证得Rt△CED≌Rt△CFD,证出CE=CF,设AE的长度为x,根据CE=CF列方程求解即可.
如图, 连接BD、AD,过点D作DF⊥CB于点F.
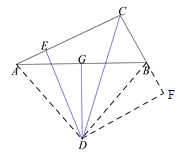
∵![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 的平分线
的平分线![]() 于点
于点![]() ,DE⊥AC,DF⊥BC,
,DE⊥AC,DF⊥BC,
∴BD=AD,DE=DF.∴Rt△AED≌Rt△BFD.
∴BF=AE.
又∵∠ECD=∠FCD,∠CED=∠CFD,CA=CA,∴Rt△CED≌Rt△CFD,
∴CE=CF,
设AE的长度为x,则CE=10-x,CF=CB+BF= CB+AE= 4+x,
∴可列方程10-x=4+x,x=3,∴AE=3;
故选C.

练习册系列答案
相关题目