题目内容
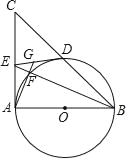
【题目】如图,在△ABC中,AB=4 cm,AC=2 cm.
(1)在AB上取一点D,当AD=_________cm时,△ACD∽△ABC.
(2)在AC的延长线上取一点E,当CE=________cm时,△AEB∽△ABC此时BE与DC有怎样的位置关系?________
【答案】16BE//DC
【解析】
(1)根据两边边对应比值相等且夹角相等得出相似三角形即可;(2)根据两边边对应比值相等且夹角相等得出相似三角形即可,再利用相似三角形的性质得出对应角之间的关系进而求出BE与DC的位置关系.
(1)当AD=1cm时(如图1),
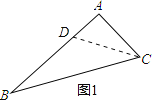
∵AB=4cm,AC=2cm,AD=1cm,
∴![]() ,
,
∵∠A=∠A,
∴△ACD∽△ABC;
(2)当CE=6cm时(如图2),
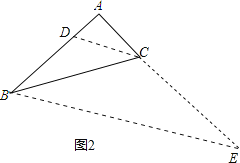
∵AB=4cm,AC=2cm,
∴![]() ,
,
∵∠A=∠A,
∴△AEB∽△ABC;
此时BE∥DC,
理由:∵△ACD∽△ABC,△AEB∽△ABC,
∴∠ACD=∠ABC=∠E,
∴BE∥CD.

练习册系列答案
相关题目