题目内容
【题目】在平面直角坐标系xOy中,直线y=-2x+1与y轴交于点C,直线y=x+k(k≠0)与y轴交于点A,与直线y=-2x+1交于点B,设点B的横坐标为x0.
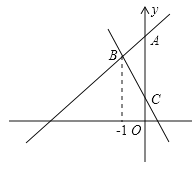
(1)如图,若x0=-1.
①求点B的坐标及k的值;
②求直线y=-2x+1、直线y=x+k与y轴所围成的△ABC的面积;
(2)若-2<x0<-1,求整数k的值.
【答案】(1)①B(-1,3),k=4;②![]() ;(2)5、6
;(2)5、6
【解析】
(1)①将x=-1代入y=-2x+1,得出B点坐标,进而求出k的值;
②求出A,C点坐标,进而得出AC的长,即可得出△ABC的面积;
(2)分别得出当x0=-2以及-1时k的值,进而得出k的取值范围.
解:(1)①当x=-1时,y=-2×(-1)+1=3,
∴B(-1,3).
将B(-1,3)代入y=x+k,得k=4.
②当x=0时,y=x+4=0,
∴A(0,4),
当x=0时,y=-2x+1=1,
∴C(0,1),
∴AC=4-1=3,
∴△ABC的面积为:![]() ×1×3=
×1×3=![]() ;
;
(2)![]() ,
,
解得
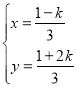 ,
,
∴x0=![]() ,
,
∴-2<![]() <-1,
<-1,
∴4<k<7.
∴整数k的值为5、6.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目