题目内容
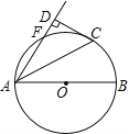
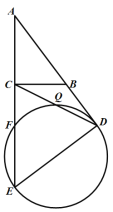
【题目】如图,在△ABC中,∠ACB=90°,AB=10,BC=6,点D在AB的延长线上,且BD=6,过点D作DE⊥AD交AC的延长线于点E,以DE为直径的⊙O交AE于点F.
(1)求⊙O的半径;
(2)设CD交⊙O于点Q,①试说明Q为CD的中点;②求BQ·BE的值.
【答案】(1)⊙O的半径为6;(2) ①证明见解析;②BQ![]() BE=36.
BE=36.
【解析】
(1)根据勾股定理求出AC,证明△ACB∽△ADE,根据相似三角形的性质求出DE,即可得到⊙O的半径;
(2)①连接EQ,根据等腰三角形的三线合一证明;
②连接BQ,根据等腰三角形的性质得到BQ⊥CD,得到B,Q,E三点共线,证明△BDQ∽△BED,根据相似三角形的性质计算即可.
(1)∠ACB=90°,AB=10,BC=6,∴AC=![]() =8.
=8.
∵∠ACB=90°,DE⊥AD,∴△ACB∽△ADE,∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,解得:DE=12,AE=20,则⊙O的半径为6;
,解得:DE=12,AE=20,则⊙O的半径为6;
(2)①连接EQ.
∵AE=20,AC=8,∴EC=ED=12.
∵DE为⊙O直径,∴∠EQD=90°,∴EQ⊥CD于Q,∴Q为CD中点;
②连接BQ.
∵BC=BD=6,Q为CD中点,∴BQ⊥CD,∴B,Q,E三点共线.
∵∠BDQ+∠EDQ=90°,∠B=∠B,∴△BDQ∽△BED,∴![]() =
=![]() ,∴BQBE=BD2=36.
,∴BQBE=BD2=36.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目