题目内容
(本题满分12分)已知:如图8,△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D作DE⊥AC于点E,交BC的延长线于点F.(12)
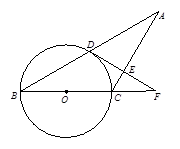
求证:(1)AD=BD; (2)DF是⊙O的切线.
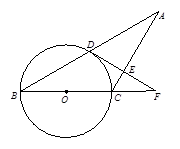
求证:(1)AD=BD; (2)DF是⊙O的切线.
(1)CD⊥AB、AC=BC、AD=BD
(2)OD⊥DF、DF是⊙O的切线
(2)OD⊥DF、DF是⊙O的切线
试题分析:证明(1)连接BD∵AC是⊙O的直径
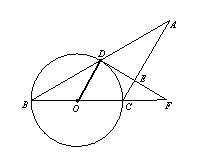
∴∠ADC=90°∴CD⊥AB∵AC=BC∴AD=BD
(2)连接OD
∵DE⊥AC
∴∠CEF=90°
∵AD=BD BO=CO
∴DO∥AC
∴∠ODF=∠CEF=90°
∴OD⊥DF
∴DF是⊙O的切线
点评:本题主要考查了切线的判定,等腰三角形的性质等知识点.要注意的是要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
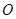 上,且BO=BC,则
上,且BO=BC,则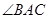 = 。
= 。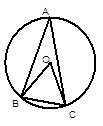
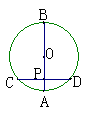
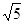


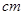 ,则扇形的面积是
,则扇形的面积是  .
.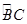 于D.
于D.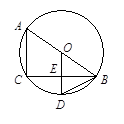
 .若将⊙P向上平移,则⊙P与x轴相切时点P的坐标为 ;
.若将⊙P向上平移,则⊙P与x轴相切时点P的坐标为 ;