题目内容
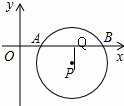
如图,平面直角坐标系中,⊙P与x轴分别交于A、B两点,点P的坐标为(3,-1),AB=2 .若将⊙P向上平移,则⊙P与x轴相切时点P的坐标为 ;
.若将⊙P向上平移,则⊙P与x轴相切时点P的坐标为 ;
 .若将⊙P向上平移,则⊙P与x轴相切时点P的坐标为 ;
.若将⊙P向上平移,则⊙P与x轴相切时点P的坐标为 ;
(3,2)
试题分析:作PQ⊥AB于点Q,连接AP,根据垂径定理及勾股定理即可求得AP的长,即可得到⊙P的半径,从而得到⊙P与x轴相切时点P的坐标.
作PQ⊥AB于点Q,连接AP
则可得
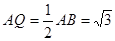 ,
,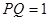
∴
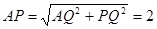 ,即⊙P的半径为2
,即⊙P的半径为2∴⊙P与x轴相切时点P的坐标为(3,2).
点评:解答本题的关键是熟练掌握垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
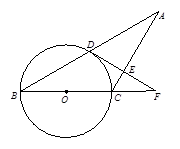
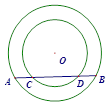
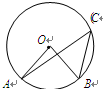
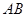 是
是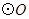 的直径,弦
的直径,弦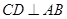 ,垂足为
,垂足为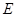 ,
,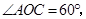
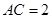 .
.
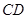 的长;
的长;