Question

【题目】在中，．

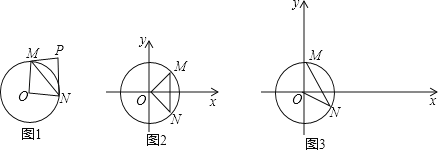
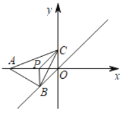
（1）如图1，若将线段绕点逆时针旋转得到线段连接则的面积；

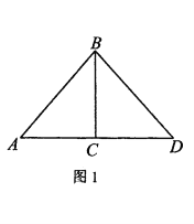
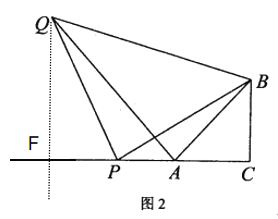
（2）如图2，点为延长线上一个动点，连接以为直角项点，为直角边作等腰直角连接，求证：；

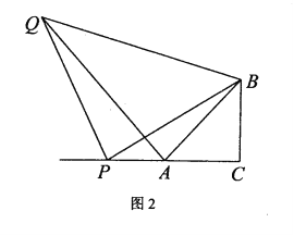
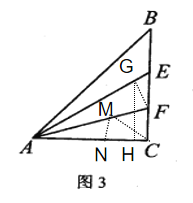
（3）如图3，点为线段上两点，且点是线段上一个动点，点是线段上一个动点，是否存在点使的值最小，若存在，求出最小值；若不存在，说明理由．

Answer 1

【答案】（1）36；（2）证明见解析；（3）存在，3．

【解析】

（1）根据勾股定理求出AB的长度，再根据旋转的性质可得，最后根据三角形面积公式求解即可；

（2）过作交的延长线于，通过证明，可得，再根据线段的和差关系可得，再根据，即可求得，即可得证；

（3）作于G，于H，通过角平分线的性质和含30°角的直角三角形的性质求得，据此求出的最小值即可．

（1）∵

∴

∵将线段绕点逆时针旋转得到线段

∴

∴；

（2）过作交的延长线于

∵是等腰直角三角形

∴，

∴

∵

∴

∴

在△QPF和△PBC中

∴

∴

∴

∵

∴

∴

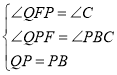
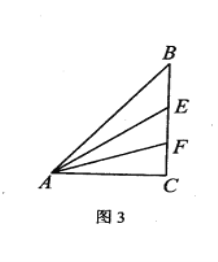
（3）存在

如图，作于G，于H

∵，，

∴，，

∵

∴

∴

故当点M、N在线段GH上时，存在最小值，最小值为3