题目内容
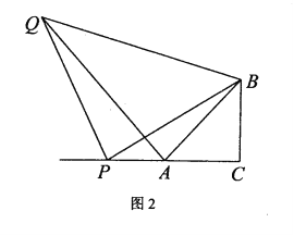
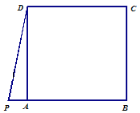
【题目】如图,正方形 ABCD 中,P 是 BA 延长线上一点,且PDA (0 45).点 A,点 E 关于 DP 对称,连接 ED,EP ,并延长 EP 交射线CB 于点 F ,连接 DF .
(1)请按照题目要求补全图形.
(2)求证:∠EDF=∠CDF
(3)求∠EDF(含有 的式子表示);
(4)过 P 做PH⊥DP交 DF 于点 H ,连接 BH , 猜想 AP 与 BH 的数量关系并加以证明.
【答案】(1)图见解析,(2)证明见解析;(3)∠EDF=45°,(4)BH=![]() .
.
【解析】
(1)根据题目条件直接作图即可;
(2)根据对称可知DE=AD,∠PAD=∠DEP=90°,易证Rt△EDF≌Rt△CDF,即可得到结论.(3)根据(2)可得∠EDF=∠CDF=![]() ∠PDC,即可得∠EDF=45°+
∠PDC,即可得∠EDF=45°+![]() ;
;
(4)作HG⊥PB,构造△PDA≌△HPG和等腰直角△HGB.由(3)得∠EDF=45°+![]() ;可得∠PDH=45°,△PDG是等腰直角三角形,得PD=PH,进而可证△PDA≌△HPG, HG=PA=BG,即可得△HGB是等腰直角三角形,所以BH=
;可得∠PDH=45°,△PDG是等腰直角三角形,得PD=PH,进而可证△PDA≌△HPG, HG=PA=BG,即可得△HGB是等腰直角三角形,所以BH=![]() PA.
PA.
(1)如图:

(2)证明:∵点A,点E关于DP对称,
∴DE=AD,∠PAD=∠DEP,
∵在正方形ABCD中,AD=CD,∠C=∠DAB=90°,
∴DE=CD,∠E=∠C=90°,
在Rt△EDF和Rt△CDF中,
![]() ,
,
∴Rt△EDF≌Rt△CDF(HL),
∴∠EDF=∠CDF.
(3)由(2)得∠EDF=∠CDF=![]() ∠PDC,
∠PDC,
又∵∠PDC=90°+2![]() .
.
∴∠EDF=45°+![]() .
.
(4)结论:BH=![]() PA.
PA.
如图:过H点作HG垂直于PB,

∵∠PDF=∠EDF-∠EPD,
∵∠EDF=45°+![]() ,∠EPD=
,∠EPD=![]() ,
,
∴∠PDF=45°.
又∵PD⊥PF,
∴△PDG是等腰直角三角形,
∴AP=HP,
又∵∠PDA+∠DPA=90°,∠PDA+∠HPA=90°,
∴∠PDA=∠HPA,
在△PDA和△HPG中,
 ,
,
∴△PDA≌△HPG(AAS)
∴PA=HG,DA=PG,
∵DA=AB
∴BG=PA,
∴△HGB为等腰直角三角形,
∴BH=![]() ,
,
∴BH=![]() PA.
PA.

【题目】在一个不透明的袋子中装有仅颜色不同的20个小球,其中红球6个,黑球14个
(1)先从袋子中取出x(x>3)个红球后,再从袋子中随机摸出1个球,将“摸出黑球”,记为事件A.请完成下列表格.
事件A | 必然事件 | 随机事件 |
x的值 |
(2)先从袋子中取出m个红球,再放入2m个一样的黑球并摇匀,随机摸出1个球是黑球的概率是![]() ,求m的值.
,求m的值.