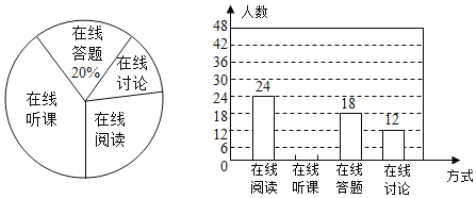
题目内容
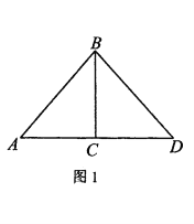
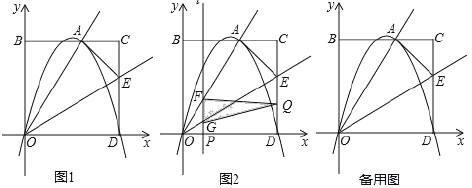
【题目】如图1，矩形OBCD的边OD，OB分别在x轴和y轴上，且B (0，8)，D(10，0)．点E是DC边上一点，将矩形OBCD沿过点O的射线OE折叠，使点D恰好落在BC边上的点A处．
（1）若抛物线y＝ax2+bx经过点A，D，求此抛物线的解析式；
（2）若点M是（2）中抛物线对称轴上的一点，是否存在点M，使△AME为等腰三角形？若存在，直接写出点M的坐标；若不存在，说明理由；
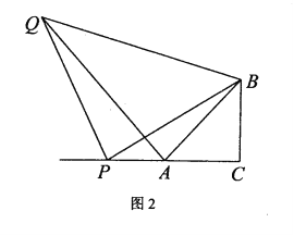
（3）如图2，动点P从点O出发沿x轴正方向以每秒1个单位的速度向终点D运动，动点Q从点D出发沿折线D﹣C﹣A以同样的速度运动，两点同时出发，当一点运动到终点时，另一点也随之停止，过动点P作直线1⊥x轴，依次交射线OA，OE于点F，G，设运动时间为t（秒），△QFG的面积为S，求S与t的函数关系式，并直接写出t的取值范围．（t的取值应保证△QFG的存在）
【答案】（1）
；（2）存在，满足要求的点M的坐标为
，(5，5)，(5，2.5)，理由见解析；（3）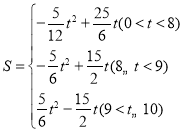
【解析】
（1）先利用矩形的性质及折叠的性质求出点A的坐标，然后用待定系数法即可求得抛物线的解析式；
（2）易求得抛物线的对称轴x＝5，过点E作ET⊥AH，垂足为T，设点M的坐标为（m，n），运用勾股定理用含n的代数式表示出AM2、EM2，然后分三种情况进行讨论：AM＝AE, EM＝EA, MA＝ME分别列出等式，求出n，就可求出点M的坐标；
（3）根据点Q的位置不同，分以下四种情况进行讨论：①点Q在线段DC上；②点Q在AC上且在直线l的右边；③点Q在AC上且在直线l上；④点Q在AC上且在直线l的左边，分情况讨论即可．
（1）解：∵四边形OBCD是矩形，B（0，8），D（10，0），
∴BC＝OD＝10，DC＝OB＝8，∠OBC＝∠C＝90°．
由折叠可得：OA＝OD＝10，AE＝DE．
∵∠OBC＝90°，OB＝8，OA＝10，
∴AB＝
，
∴AC＝4．
设AE＝DE＝x，则CE＝8﹣x，
∵∠C＝90°，
∴x2＝42+（8﹣x）2，
解得：x＝5，
∴AE＝DE＝5，
∴点A的坐标为（6，8），点E的坐标为（10，5）．
∵抛物线y＝ax2+bx经过点A（6，8），D（10，0），
∴
解得
此抛物线的解析式为；
（2）存在M，使△AME为等腰三角形．
设抛物线的对称轴与BC交于点H，过点E作ET⊥AH，垂足为T，连接AM、ME，如图1，
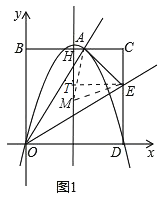
设点M的坐标为（m，n），则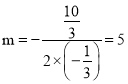
，
∴AH＝6﹣5＝1，HM＝8﹣n，ET＝10﹣5＝5，TM＝5﹣n
∵AH⊥HM，
∴AM2＝AH2+MH2＝1+（8﹣n）2
∵ET⊥MH
∴ME2＝ET2+MT2＝25+（5﹣n）2
①若AM＝AE，则AM2＝AE2，
∴1+（8﹣n）2＝25，
∴（8﹣n）2＝24，
解得：
，
此时点M的坐标为
或 
；
②若EM＝EA，则EM2＝EA2
∴25+（5﹣n）2＝25
∴（5﹣n）2＝0
∴n3＝5
此时点M的坐标为
；
③若MA＝ME，则MA2＝ME2
∴1+（8﹣n）2＝25+（5﹣n）2
解得：n4＝2.5
此时点M的坐标为
；
综上所述：满足要求的点M的坐标为，（5，5），（5，2.5）；
（3）设直线OA的解析式y＝k1x，
∵点A的坐标为（6，8），
∴6k1＝8，
∴
，
∴直线OA的解析式为
，
同理可得：直线OE的表达式为y＝
，
∵OP＝1×t＝t
∴P（t，0）
∵直线l⊥x轴于点P，点F，G是直线l与OA，OE的交点
∴
，
故
，
①当0＜t＜8时，点Q在线段DC上，
过点Q作QS⊥直线l，垂足为S，
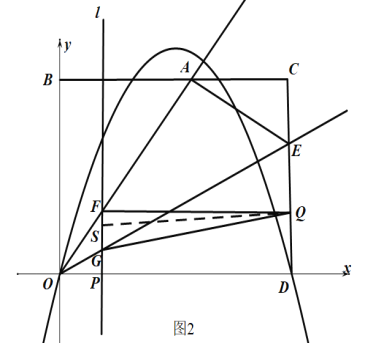
则QS＝PD＝10﹣t
∴
＝
＝
；
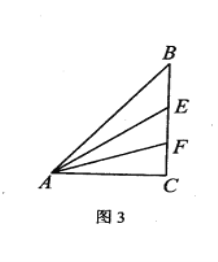
②当8≤t＜9时，点Q在线段CA上，且在直线l的右侧，
设FG交AC于点N，如图3，
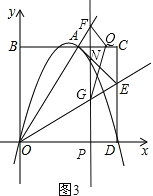
则QN＝CN﹣CQ＝PD﹣CQ＝（10-t）﹣（t﹣8）＝18﹣2t
∴
＝
＝
；
③当t＝9时，QN＝18﹣2t＝0，点Q与点N重合，此时△QFG不存在，故舍去；
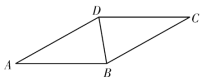
④当9＜t≤10时，点Q在线段CA上，且在直线l的左侧，设FG交AC于点N，如图4．
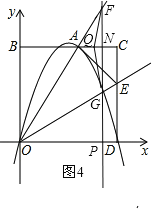
则QN＝CQ﹣CN＝CQ﹣PD＝（t-8）-(10-t)＝2t﹣18
∴
＝
＝
;
综上所述：．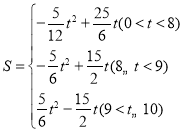
