题目内容
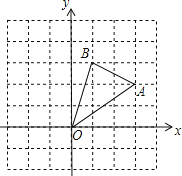
【题目】如图,点![]() ,点
,点![]() 是射线
是射线![]() 上一动点(不与
上一动点(不与![]() 点重合),过点
点重合),过点![]() 作直线
作直线![]() 的平行线交
的平行线交![]() 轴于
轴于![]() ,过点
,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于
于![]() ,连结
,连结![]() ,
,![]() ,
,![]() .
.
(1)当点![]() 在线段
在线段![]() 上且
上且![]() 时,
时,![]() __________.
__________.
(2)当![]() 与
与![]() 相似时,
相似时,![]() 点的横坐标为____________.
点的横坐标为____________.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
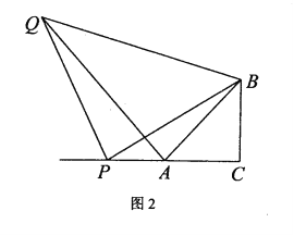
(1)设BC与OP交于点D,先证出四边形PBOC为平行四边形,设BP=OC=OP=x,根据勾股定理求出CP和AP,然后根据AP+OP=1即可求出x,再根据勾股定理求出AB和BC即可求出结论;
(2)根据点P的位置分类讨论,分别画出对应的图形,分别根据勾股定理求出AB、BC和AC,然后根据相似的性质可得三角形ABC为等腰直角三角形,从而求出结论.
解:(1)设BC与OP交于点D
∵CO⊥x轴,BP⊥x轴
∴CO∥BP
∵CP∥OB
∴四边形PBOC为平行四边形
∴BP=OC,BC=2CD,OD=![]() OP
OP
∵点B在y=x上
∴BP=OP
设BP=OC=OP=x
∴CP=![]() x
x
∴AP= CP=![]() x
x
∵点A的坐标为(-1,0)
∴AP+OP=1
即![]() x+x=1
x+x=1
解得:x=![]() -1
-1
∴BP=OC=OP=![]() -1,AP=2-
-1,AP=2-![]() ,OD=
,OD=![]()
根据勾股定理可得AB=![]()
CD=![]() =
=![]()
∴BC=![]()
∴![]()
![]()
故答案为:![]() .
.
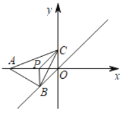
(2)①当点P在线段OA上时,

由(1)可知,△OPC为等腰直角三角形,设BP=OC=OP=x(0<x<1),则AP=1-x
根据勾股定理:AC=![]() ,
,
AB=![]() ,
,
BC=2CD=2![]() =2
=2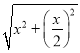 =
=![]()
∵1-x<1,
∴AB<AC
若![]() 与
与![]() 相似时,
相似时,
∴△ABC为等腰直角三角形,其中AB和BC为直角边
即![]()
解得:x1=![]() ,x2=-1(不符合x的取值范围,故舍去)
,x2=-1(不符合x的取值范围,故舍去)
即OP=![]()
∵点P在OA上
∴点P的横坐标为![]() ;
;
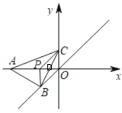
当点P在AO的延长线上时,
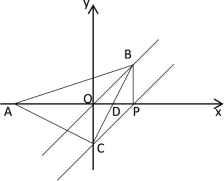
同理可证:四边形OCPB为平行四边形,△OPC为等腰直角三角形,设BP=OC=OP=y(y>0),则AP=1+y
根据勾股定理:AC=![]() ,
,
AB=![]() ,
,
BC=2CD=2![]() =2
=2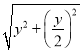 =
=![]()
∵1+y>1,
∴AB>AC
若![]() 与
与![]() 相似时,
相似时,
∴△ABC为等腰直角三角形,其中AC和BC为直角边
即![]()
解得:y1=![]() ,y2=
,y2=![]() (不符合y的取值范围,故舍去)
(不符合y的取值范围,故舍去)
即OP=![]()
∵点P在AO延长线上
∴点P的横坐标为![]() .
.
综上:点P的横坐标为![]() 或
或![]() .
.
故答案为:![]() 或
或![]() .
.