题目内容
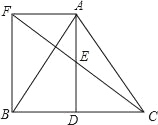
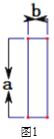
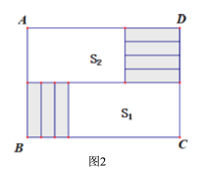
【题目】将7张相同的长方形纸片(如图1)按图2所示的方式不重叠地放在长方形ABCD内,未被覆盖的部分恰好可以分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.
(1)当a=9,b=2,AD=30时,S1-S2=______.
(2)当AD=30时,用含a,b的式子表示S1-S2.
(3)若AB长度不变,AD变长,将这7张小长方形纸片按照同样的方式放在新的长方形ABCD内,而且S1-S2的值总保持不变,则a,b满足的关系是______.
【答案】(1)48;(2)30a-120b+ab;(3)a=4b.
【解析】
(1)观察图形,分别求出S1和S2的面积,再求差即可;
(2)用含a、b的代数式分别表示S1和S2的面积,再求差即可;
(3)设AD=m, 用含a、b、m的代数式分别表示S1和S2的面积差,再去括号合并同类项,根据题意S1-S2的值总保持不变,即可解答.
(1)解:当a=9,b=2,AD=30时,S1=a(30-3b)=9×(30-3×2)=216
S2=4b(30-a)=4×2×(30-9)=168
S1-S2=216-168=48
(2)解:S1-S2
=a(30-3b)-4b(30-a)
=30a-120b+ab
(3)解:设AD=m,
S1-S2
=(am-3ab)-(4bm-4ab)
=am-4bm+ab
若S1-S2的值总保持不变,则S1-S2的值与m的取值无关,所以有am-4bm=0
则a=4b.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目