题目内容
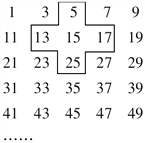
【题目】将连续的奇数1，3，5，7，9，…，排成如图所示的数阵．
（1）十字框中的五个数的和与中间数15有什么关系？
（2）设中间数为
，求出十字框中五个数之和；
（3）十字框中五个数之和能等于2 015吗？若能，请写出这五个数；若不能，说明理由．
【答案】（1）15的5倍（2）5a（3）能
【解析】试题分析：（1）将十字框中的五个数相加即可得出结论；
（2）结合（1）将15替换成a，则可得出结论；
（3）设中间的数为x，其它4个数分别为x﹣10、x﹣2、x+2、x+10，令其相加等于2015算出x的值，结合数阵数的特点即可得出结论．
试题解析：解：（1）∵5+13+15+17+25=75=5×15，∴十字框中的五个数的和是中间数15的5倍；
（2）由（1）可知：若中间数为a，则十字框中五个数之和5a；
（3）能．理由如下：
设中间的数为x，其它4个数分别为x﹣10、x﹣2、x+2、x+10，5个数之和为x﹣10+（x﹣2）+x+（x+2）+（x+10）=5x=2015，解得x=403，∵403为奇数，且在数阵的第400行第二列，∴存在五个数之和等于2015，五个数分别为：393、401、403、405、413．
练习册系列答案
相关题目
